-
Type
-
Livre
-
Cours d'algèbre
-
Cours de géométrie
-
Sujet
-
Algèbre
-
Description
-
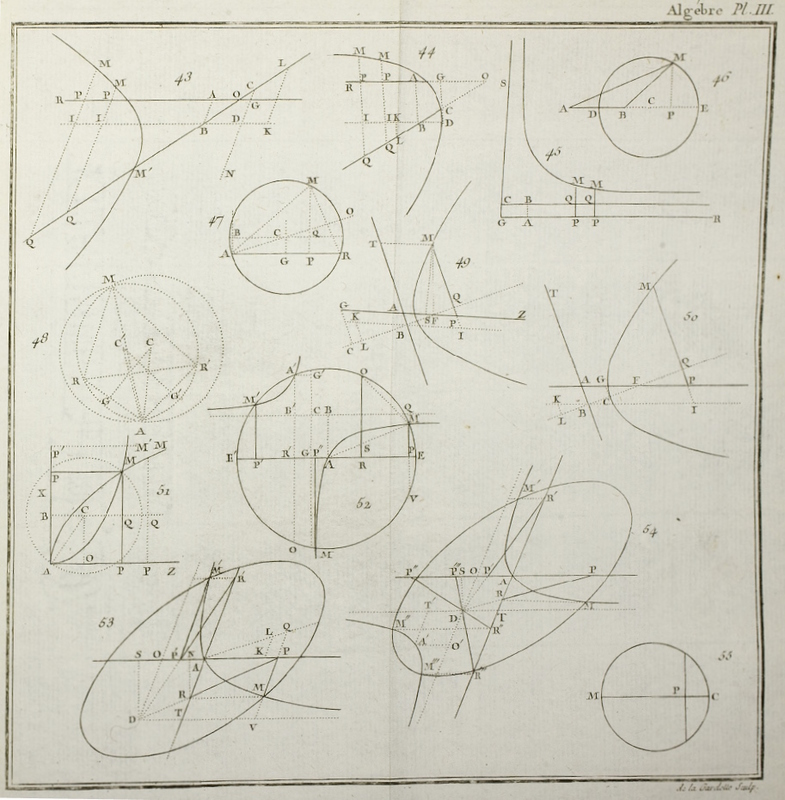
1781. Ph,-D, PIERRES, 1781, 316 pages. 3 planches, 55 figures. Leçons 1 à 340.
-
Date
-
1770
-
1781
-
1797
-
Editeur
-
Paris : Imprimerie royale. 1770
-
Paris : De l’Imprimeur Ph,-D, PIERRES, Imprimeur ordinaire du Roi, rue S. Jacques. 1781
-
Paris : Richard & Caille. 1797
-
Table des matières
-
Pagination d'après l'édition de 1781
PREMIÈRE SECTION.
Dans laquelle on donne les principes du calcul algébrique. 1
Ce que c'est que l'Algebre, 1
Des opérations fondamentales sur les quantités considérées généralement, 3
De l'addition et de la soustraction, 3
Comment on indique ces opérations, 3
Coefficiens, ce que c'est, 4
Ce qu'on appelle Termes d'une quantité, 6
Ce que c'est que Monome, Trinome & Polynome, 6
Signes des quantités positives ; & des quantités négatives, 7
De la Multiplication, 7
Comment on indique cette opération pour les monomes, 8
Ce que c'est qu'un Exposant, 9
Comment on indique la multiplication des quantités complexes ou polynomes, 15
De la Division, 16
Comment on indique cette opération, 16
Ce que c'est qu’une quantité qui a zéro pour exposant, 17
De la manière de trouver le plus grand commun diviseur de deux quantités littérales, 23
Des fractions littérales, 25
Des Equations, 29
Du signe d'égalité & des membres d'une équation, 29
Des Equations du premier degré à une seule inconnue, 31
Règle pour la transposition des quantités d’un membre de l'équation dans l’autre, 31
Règle pour dégager l’inconnue de son multiplicateur, 33
Règle pour faire disparoitre les dénominateurs, 35
Application des princes précédens, à la résolution de quelques questions simples, 37
Règle pour mettre une question en équation, 38
Des quantités positives & négatives; ce que c'est & ce qu'elles indiquent, 47
Des Équations du premier degré à plusieurs inconnues, 53
Règle pour éliminer les inconnues, 54
Autre méthode pour éliminer les inconnues, 59
Application des règles précédentes, à la résolution de quelques questions qui renferment plus d'une inconnue, 61
Des cas où les questions proposées restent indéterminées, quoiqu'on ait autant d’équations que d’inconnues; & des cas où les questions sont impossibles, 68
Des problèmes indéterminés, 71
Des Equations du second degré à une seule inconnue, 76
Signe radical; ce que c’est, 76
Pourquoi toute Equation du second degré a toujours deux racines, 77
Quand est-ce que ces deux racines font imaginaires ou impossibles, 78
Préparations nécessaires pour la résolution d'une Equation du
second degré, 79
Règle pour la résolution d’une Equation du second degré, 80
Application de cette règle à la résolution de quelques questions, 82
De la formation des puissances des quantités monomes, de l'extraction de leurs racines, & du calcul des radicaux & des exposans, 89
Règle pour élever un monome à une puissance proposée, 89
Règle pour extraire une racine d'un degré proposé d'une quantité monome, 91
Règle pour réduire à un même, tous les exposans de différens radicaux, 96
Règle pour faire passer une quantité du numérateur au dénominateur & réciproquement, 100
De la formation des puissances des. quantités complexes, & de l’extraction de leurs racines, 101
Formation des puissances des binomes, 101
Formation de puissances des polynomes, 111
De l'extraction des racines des quantités complexes, 113
De la manière d'approcher de la racine des puissances imparfaites des quantités littérales, 118
Des Equations à deux inconnues, lorsqu'elles passent le premier degré, 114
Des Equations à deux termes, 116
Des Equations qui peuvent se résoudre à la manière de celles du second degré, 128
De la composition des Equations, 129
Du nombre des racines d’une Equation quelconque, 129
Du rapport qu'il y a entre les racines d’une Equation, & les coëfficiens de ses différens termes, 133
Des transformations qu’on peut faire subir aux Equations, 136
Règle pour faire disparaitre les dénominateurs sans donner un coëfficient au premier terme, 136
Règle pour faire disparoitre le second terme d'une Equation, 137
De la réfolution générale des Equations composées, 138
Application de la méthode au troisième degré, 140
Cas irréductible , ce que c'est, 141
Pour le quatrième degré, 143
Des diviseurs commensurables des Equations, 144
De la manière d'approcher des racines des Equations composées, 148
SECONDE SECTION, 151
Dans laquelle on applique l'Algèbre à l'Arithmétique & à la Géométrie, 153
Comment la traduction algébrique de l’énoncé d'une propriété quelconque, conduit à la résolution d'autant de questions , que cet énoncé comprend de quantités différentes, 153
Propriétés générales des progressions arithmétiques, 153
De la sommation des puissances des termes d'une progression arithmétique quelconque, 160
Application au nombre de boulets d'une pile quadrangulaire & oblongue, 163
Formation de quelques autres suites, 164
Application au nombre des boulets d'une pile triangulaire, 167
Propriétés & usages des progressions. géométriques, 168
De la construction géométrique des quantités algébriques, 173
Construction des quantités rationnelles & d'une dimension, 174
Construction des quantités rationnelles de deux dimensions, 177
Construction des quantités rationnelles de trois dimensions, 177
Construction des quantités radicales du second degré, 179
Diverses questions de Géométrie, & réflexions tant sur la manière de les mettre en équations, que sur les diverses solutions que donnent ces équations, 185
Règle pour se déterminer sur le choix de la ligne qu'on doit prendre pour inconnue dans une question, 200
Autres applications de l'algèbre à diverses objets, 210
Des lignes courbes, en général; & en particulier des sections coniques, 217
Comment l'équation d'une Courbe sert à décrire cette courbe par points, & à en découvrir les propriétés, 218
De l'Ellipse, 224
Diverses manières de décrire cette courbe, 226
Ce que c’est que les axes , les foyers & les sommets des axes, 227
Ce que c'est que le paramètre, 228
Comparaison du cercle & de l'ellipse, 230
Manière de mener une tangente à l’ellipse, 231
Détermination de la soutangente, de la tangente, de la sounormale & de la normale, 232
Diamètres conjugués de l'ellipse, ce que c'est; les propriétés de leurs ordonnées, 236
Propriétés des diamètres conjugués, 237
Manière de déterminer les axes, par les diamètres conjugués & l'angle qu'ils comprennent, 248
De l'Hyperbole, 243
Diverses manières de décrire cette courbe, 244
Ce que c’est que les axes, les foyers & les sommets des axes de l'hyperbole, 245
Paramètre de l'Hyperbole, 246
Manière de mener une tangente à l’hyperbole, 248
Détermination de la soutangente, la tangente, la sounormale & la normale 249
Des asymptotes, ce que c'est & comment on les détermine, 251
Diamètre conjugué de l'hyperbole; ce que c'est, 256
Propriétés de leurs ordonnées, 257
Propriétés des diamètres conjugués, 259
Manière de décrire l'hyperbole quand on connoît les diamètres conjugués & l'angle qu'ils forment, 260
De l’hyperbole entre les asymptotes, 260
Puissance de l'hyperbole; ce que c'est, 261
Propriétés des lignes tirées entre les asymptotes de l'hyperbole & la courbe, 262
Manière de décrire l'hyperbole, lorsqu’on connoit les asymptotes & un point de la courbe, 264
De la Parabole, 265
Ce que c'est que l’axe, le sommet, le foyer, la directrice & le paramètre, 265
Manières de décrire cette courbe, 266
Propriétés de ses ordonnées à l'axe, 267
De la tangente, Ia soutangente, la sounormale de la parabole, 267
Des diamètres de la parabole & de leur paramètre, 269
Propriétés de la parabole par rapport à ses diamètres, 270
Manière de décrire Ia parabole, lorsqu'on connoît un diamètre, & l'angle qu'il forme avec la tangente au sommet de çe diamètre, 270
Génération des sections coniques dans le cône, 271
Réflexions sur les équations aux sections coniques , & caractères distinctif de ces équations, 272
Moyens de amener aux sections coniques toute équation du second degré à deux indéterminées, lorsqu'elle exprime une chose possible, 281
Application de ce qui précède à Ia résolution de quelques queslions indéterminées, 295
Application des mêmes principes à quelques questions déterminées, 306
Fin De La Table Des Matieres.
EXTRAIT DES REGISTRES DE L’ACADÉMIE ROYALE DES SCIENCES
Du 20 Décembre 1769.
3 planches
-
Titre
-
II. Cours de mathématiques, À l'usage du Corps royal de l'Artillerie. Tome second. Contenant l’Algèbre & l'Application de l'algèbre à la géométrie
Bézout, Étienne (1730-1783)
III. Cours de mathématiques à l'usage des Gardes du pavillon et de la Marine. Troisième partie. Contenant l'Algèbre & l'application de cette science à l'Arithmétique & à la Géométrie.
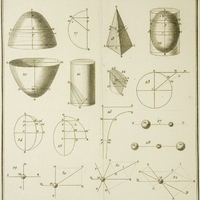III. Cours de Mathématiques à l'usage du Corps royal de l'Artillerie. Tome troisième. Contenant les Principes généraux de la Mécanique et l'Hydrostatique. Précédés des Principes de calcul qui servent d'introduction aux Sciences physico-mathématiques
I. Cours de Mathématiques, À l'usage du Corps royal de l'Artillerie. Tome premier. Contenant l’Arithmétique, la Géométrie & la Trigonométrie rectiligne