-
Type
-
Livre
-
Cours d'analyse
-
Cours de mécanique
-
Description
-
1772. Paris. Imprim. royale. 381 pages. 6 planches 174 figures. Leçons 1 à 349
1788. Paris. Ph.D. Pierres. 381 pages. 6 planches. Leçons 1 à 349
1799 an VII. Paris. Richard, Cailles, Ravier, 368 pages. 4 planches, 69 figures. Leçons 1 à 349
-
Date
-
1772
-
1788
-
1799
-
Editeur
-
Paris : Imprimerie Royale. 1772
-
Paris : DE l'IMPRIMERIE DE PH.-D. PIERRES, Premier Imprimeur Ordinaire du Roi, rue S. Jacques. 1788
-
Paris : Chez RICHARD, CAILLES & RAVIER, Libraires, rue Haute-Feuille, N°. 11, au coin de la rue Serpente. 1799 an VII
-
Table des matières
-
D'après Paris. Impr. royale. 1772
381 pages, 6 planches, 1 table, 349 leçons
-page j-
TABLE DES MATIÈRES.
PRINCIPES DE CALCUL qui servent d'introduction aux Sciences Physico-mathématiques.
NOTIONS préliminaires, 1
Ce qu'on doit entendre par Élémens , Variations , où accroissemens infiniment petits des quantités, 2
Ce que l'on entend. par quantités infiniment petites, ou infinies ; & de la subordination qu'on doit mettre entre ces quantités, dans le calcul, 3
Élémens du Calcul différenciel,
Ce qu'on entend par Différence , Différencielle, & la manière d'indiquer la différencielle d’une quantité, 10
Comment on trouve la différencielle d'une quantité dont toutes les parties sont simples ou linéaires, 11
Règle pour différencier un produit dont tous les facteurs sont inégaux, 12
Règle pour différencier les puissances, 14
Applications de ces règles à la différenciation de plusieurs sortes de quantités, 15
Des différences secondes, troisièmes, &c. 15
Comment on indique ces différences, 18
Comment on les détermine, 19
Remarque sur le signe qu’on doit donner aux différencielles des quantités qui décroissent , par rapport au signe de celles qui croissent, 22
Des différencielles de Sinus & Cosinus; ce que c'est, & comment on les trouve, 23
-page ij-
Des différencielles Logarithmiques, 26
Règle pour trouver la différencielle du Logarithme d’une quantité quelconque, 29
Des différencielles des quantités exponencielles, 31
Application des Règles précédentes,
1.° Aux Soutangentes, Tangentes, Soufnormales, &c. des Lignes courbes, p. 33
2.° Aux limites des lignes courbes , & en général aux limites des quantités, & aux questions de Maximus & Minimus, 42
3.° Aux Rayons de Courbure , ou de la Développée, 63
Élémens du Calcul intégral, Quel est l’objet de ce calcul, 68
Ce qu'on entend par fonction d'une quantité, 69
Comment on indique l’intégrale d’une quantité, 69
Règle fondamentale pour intégrer les différencielles monomes à une seule variable, 70
Remarque sur la constante qu’on doit ajouter à toute intégrale, 72
Des différencielles complexes dont l'intégration rentre dans la règle fondamentale, 73
Des différencielles binomes qui peuvent s'intégrer algébriquement, 76
Application des Règles précédentes ,
1.° A la quadrature des courbes, 84
2.° A la rectification des lignes courbes, 92
3.° Aux surfaces courbes, 95
4.° A la mesure des solidités, 97
Toisé de l’entonnoir d’une mine, 102
De l'intégration des quantités qui renferment des sinus & des cosinus, 105
De la manière d'intégrer par approximation , & quelques usages de cette méthode, 108
Application à la rectification du cercle, 109
-pageiij -
Application à la recherche des logarithmes, 116
Usages des approximations précédentes pour l’intégration des diverses quantités, 127
De la manière de ramener (lorsque cela et possible) l’intégration d’une différencielle binome proposée, à celle d’une autre différencielle binome connue, 139
Des Fractions rationnelles, 146
Ce qu’on doit faire pour les intégrer, lorsque tous les facteurs du dénominateur sont réels & inégaux, 148
Comment on doit procéder à l'intégration, lorsque quelques-uns des facteurs du dénominateur sont égaux, 150
Comment on trouve les coefficiens des fractions partielles, dans lesquelles on doit décomposer la fraction qu'il s'agit d'intégrer, 152
Ce qu’on doit faire lorsque le dénominateur a des facteurs imaginaires, 156
De quelques Transformations qui peuvent faciliter les intégrations, 160
De l'intégration des quantités exponentielles, 164
De l'intégration des quantités à deux ou à un plus grand nombre de variables, 166
Des équations différencielles, 171
Des quantités & des équations différencielles des deuxième, troisième, &c ordre, 184
PRINCIPES généraux de la Mécanique.
Notions préliminaires, 195
Ce que c’est que la Mécanique; définitions du mouvement, d’un corps, d’une force ou puissance, de l'équilibre, du repos, 195
Première loi du mouvement, 196
-page iv-
Du mouvement uniforme, ce que c’est, 197
Ce que c'est que la vitesse, 197
Mesure de la vitesse, dans de mouvement uniforme, 198
Mesure de l'espace & du temps, dans le mouvement uniforme, 198
De la manière de comparer ces trois choses, l’espace, la vitesse & le temps, pour deux corps mus d'un mouvement uniforme, 199
Des forces & de la quantité de mouvement, 200
Ce que l’on entend par la masse d’un corps, 200
Mesure de la quantité de mouvement, 201
Rapports des forces , des masses & des vitesses, 202
Ce que l’on entend par la densité d'un corps, 203
Comment on la mesure, 204
Des mouvemens uniformément accélérés, 204
Rapport des vitesses aux temps, dans le mouvement uniformément accéléré, 205
Comparaison de l’espace décrit en vertu du mouvement accéléré, avec l’espace décrit uniformément dans le même temps, en vertu de la vîtesse acquise par l’accélération , 207
Comparaison des espaces décrits d’un mouvement uniformément accéléré, 208.
Comparaison des espaces, des temps & des vitesses dans ce même mouvement, ibid.
Du mouvement libre des corps pesans , p.209.
Ce que c’est que la pesanteur; suivant quelle direction elle agit; quelle est l’intensité de cette force à différentes dislances du centre de la terre & à différentes distances de l’équateur, 209
La vitesse qu'elle communique aux différentes parties de la matière, ne dépend point de leur nombre, & par conséquent de la masse, 211
Différence entre la pesanteur & le poids. 211
La masse des corps est proportionnelle à leur poids, 212
-page v-
Les loix du mouvement libre des corps pesans font celles du mouvement uniformément accéléré, 213
Comment on détermine l’espace décrit , & la vitesse acquise par un corps grave, dans un temps donné, 214
Des mouvemens variés de quelque manière que ce soit, 217
De l'équilibre entre des forces directement opposées, 222
Principe fondamental de cet équilibre, 224
Du mouvement composé, 226
Principe fondamental de ce mouvement, 227
De la composition & de la décomposition des forces, 234
Différentes manières d’exprimer le rapport entre deux forces composantes & leur résultante, 239
Composition & décomposition des forces dont les directions sont parallèles, 241
Des momens & de leur usage pour la composition & la décomposition des forces, 245
Comment on en déduit la position & la grandeur de la résultante de plusieurs forces dirigées dans un même plan, 250
Des forces qui agissent dans des plans différens, 257
Elles peuvent toujours, lorsqu’elles sont parallèles, être réduites à une seule; & comment on y parvient, 257
Lorsqu'elles ne font point parallèles, elles peuvent toujours être réduites à deux, dont l’une sera dirigée dans un plan connu, & l’autre sera perpendiculaire à ce plan, 262
Il est souvent plus commode de les réduire à trois, perpendiculaires à trois plans connus : cela se peut toujours; & comment, 263
Des centres de gravité, 265
Ce que c’est que le centre de gravité d’un corps; & ce qu'on entend par système de corps, 265
-page vj-
Comment on détermine la distance du centre commun de gravité de plusieurs corps, à une ligne droite, 267
Ce que c’est que les axes de momens, 269
Propriété de ces axes, qui démontre que le centre de gravité d’un corps est un point unique, 270
À quoi se réduit la recherche du centre de gravité dans quelque cas que ce soit, 272
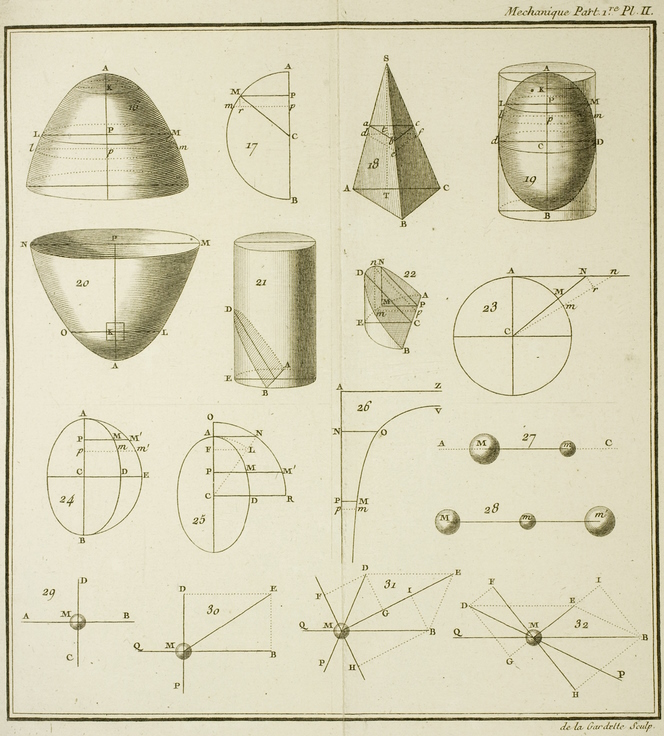
Application de ces principes à la recherche des centres de gravité de différens corps , 270—297.
Propriétés des centres de gravité , par rapport au mouvement des corps, 298
Principe général de l’équilibre des corps, 308
Principe général du mouvement, 311
Conséquences qui résultent des deux principes précédens , par rapport au mouvement du centre de gravité des corps, 311
DE L'ÉQUILIBRE DES FLUIDES, & des Corps solides qui y sont plongés.
Le premier principe de cet équilibre se tire de l’expérience; en quoi il consiste, 318
Conséquences de ce principe, quant à la manière dont la pression se transmet dans des fluides, & la direction suivant laquelle elle agit sur les parois des vases qui les renferment, 319
Comment on détermine la pression qu’un fluide pesant exerce sur une surface horizontale donnée, 324
Loi de l’équilibre entre des liqueurs de différente densité, 324
Manière d’estimer la pression sur une surface plane inclinée, 327
Des effets de la pression des fluides, estimés tant dans le sens horizontal, que dans le sens vertical, 329
-page vij-
Un corps plongé dans un fluide, y perd une partie de son poids égale au poids du volume de fluide qu'il déplace, 334
Différens moyens pour déterminer la pesanteur spécifique des corps, 341
Des fluides élastiques, 350
Du poids de l'air, 353
Du ressort de l’air, 354
Comment on détermine la densité de l’air, à différentes hauteurs, 363
Des pompes, 365
Table des pesanteurs spécifiques de différentes matières solides ou fluides, 378
Fin de la Table des Matières.
-
Titre
-
III. Cours de Mathématiques à l'usage du Corps royal de l'Artillerie. Tome troisième. Contenant les Principes généraux de la Mécanique et l'Hydrostatique. Précédés des Principes de calcul qui servent d'introduction aux Sciences physico-mathématiques
Bézout, Étienne (1730-1783)
IV. Cours de mathématiques à l'usage des Gardes du Pavillon et de la Marine. Quatrième partie. Contenant les Principes généraux de la Mécanique, précédés des Principes de calcul qui servent d'introduction aux Sciences physico-mathématiques
IV. Cours de mathématiques à l'usage du Corps royal de l'Artillerie. Tome quatrième. Contenant l'application des principes généraux de la mécanique, à différents cas de mouvement et d'équilibre.
II. Cours de mathématiques, À l'usage du Corps royal de l'Artillerie. Tome second. Contenant l’Algèbre & l'Application de l'algèbre à la géométrie