-
Type
-
Livre
-
Cours de géométrie
-
Sujet
-
Géométrie descriptive
-
Description
-
Ce texte daté de l'an III (septembre 1798 à septembre 1799) de Gaspard Monge est considéré comme fondateur de la géométrie descriptive ultérieurement enseignée par plusieurs acteurs parmi lesquels Hachette, Olivier, Poncelet, Bergery et de nombreux autres dans une variété d'écoles. Le livre de Monge débute par l'avertissement suivant (l'orthographe d'époque est respectée):
"Ce traité renferme une théorie complète de la partie de la géométrie qu’on à nommée Géométrie descriptive. Le citoyen G. Monge devoit en faire l'application aux constructions de la perspective linéaire, à la détermination des ombres dans les dessins , à la description des élémens des machines, etc., ainsi que cela est annoncé dans le programme qui précède cet écrit. Déja il avoit fait graver les dessins qui servent maintenant de modèles aux élèves de l’école polytechnique pour l’étude de la coupe des pierres, de la charpente, de la perspective et des ombres; mais les différentes missions qu’il a reçues du gouvernement, celle qu’il remplit maintenant en Égypte, ont empêché de terminer ce travail. On a pensé qu’il seroit utile de publier séparément la première partie de cet ouvrage ; elle pourra mettre le lecteur en État d'en faire Iui-même les applications. Pour lire ce traité, il suffit de connoître la première partie de la géométrie élémentaire.
La géométrie descriptive a deux objets : le premier, de donner les méthodes pour représenter sur une feuille de dessin qui n’a que deux dimensions, savoir, longueur et largeur, tous les corps de la nature; qui en ont trois, longueur, largeur et profondeur, pourvu néanmoins que ces corps puissent être définis rigoureusement. Le second objet est de donner la manière de reconnoître d’après une description exacte les formes des corps, et d’en déduire toutes les vérités qui résultent et de leur forme et de leurs positions respectives."
Le titre de Monge va connaitre de successives et multiples versions. La géométrie descriptive réunit en une seule dénomination un ensemble d'éléments précédemment connus. Les problèmes qu'elle entend éclairer de nouvelle manière sont ceux qui sont posés dans les métiers de la taille des pierres, de la conception de charpente, de l'usinage et, plus généralement, des métiers mettant en œuvre les métaux en feuille. Le dessin linéaire, la cartographie, le tracé des ombres, la perspective et de manière plus générale la projection sur des plans d'objets en trois dimensions se montrent étudiés de manière théorique et pratique. On notera l'arrêt de parution suite à la chute de l'Empire (1814).
Les éditeurs suivants sont notés :
1/ Paris : Baudouin, 1798, an III
2/ Paris : Baudouin, 1802, an VII
3/ Paris : J. Klostermann fils, 1811
-
Auteur
-
Monge, Gaspard (1746-1818)
-
Date
-
1798
-
Editeur
-
Paris : Baudouin, an VII
-
Table des matières
-
D'après l'édition de l'an III (1798)
- I -
Objet de la géométrie descriptive.
Considérations d'après lesquelles on détermine la position d'un point situé dans l'espace.
Comparaison de la géométrie descriptive avec l'algèbre.
Convention propre à exprimer les formes et les positions des surfaces.
Application au plan.
Solutions de plusieurs questions élémentaires relatives à la ligne droite et au plan.
- II -
Des plans tangents aux surfaces courbes, et de leurs normales.
Méthode pour mener des plans tangents par des points donnés sur les surfaces.
Des conditions qui déterminent la position du plan tangent à une surface courbe quelconque ; observation sur les surfaces développables.
Des plans tangents aux surfaces, menés par des points donnés dans l'espace.
Du plan tangent à la surface d'une ou de plusieurs sphères.
Propriétés remarquables du cercle, de la sphère, des sections coniques et des surfaces courbes du second degré.
Du plan tangent à une surface cylindrique, conique, à une surface de révolution, par des points donnés hors de ces surfaces.
- III -
Des intersections des surfaces courbes.
Définitions des courbes à double courbure.
Correspondance entre les opérations de la géométrie descriptive et celles de l'élimination algébrique.
Méthode générale pour déterminer les projections des intersections de surfaces. Modification de cette méthode dans quelques cas particuliers.
Des tangentes aux intersections de surfaces.
Intersection des surfaces, cylindrique, conique, etc.
Développement de ces intersections lorsque l'une des surfaces auxquelles elles appartiennent est développable.
Méthode de Roberval pour mener une tangente à une courbe qui est donnée par la loi du mouvement d'un point générateur.
Application de cette méthode à l'ellipse et à la courbe résultante de l'intersection de deux ellipsoïdes de révolution, qui ont un foyer commun.
- IV -
Applications des intersections des surfaces à la solution de diverses questions.
- V -
Considérations générales sur l'étendue.
Des courbes planes et à double courbure, de leurs développées, de leurs développantes, de leurs rayons de courbure.
De la surface qui est le lieu géométrique des développées d'une courbe à double courbure ; propriété remarquable des développées, considérées sur cette surface.
Génération d'une courbe quelconque à double courbure par un mouvement continu.
Des surfaces courbes.
Démonstration de cette proposition : "Une surface quelconque n'a dans chacun de ses points que deux courbures ; chacune de ces courbures a un sens particulier, son rayon particulier, et les deux arcs sur lesquels se mesurent ces deux courbures sont à angle droit sur la surface.
Des lignes de courbure d'une surface quelconque ; de ses centres de courbure, et de la surface qui en est le lieu géométrique.
Application à la division des voûtes en voussoirs et à l'art du graveur.
Additions
1 - Trois surfaces cylindriques à bases circulaires, qui se coupent, ont en général huit points communs.
2 - De la génération de la surface gauche. (C'est ainsi qu'on appelle la surface qui enveloppe l'espace parcouru par une droite).
De la surface gauche qui peut être engendrée par une droite de deux manières différentes.
3 - Du plan tangent à une surface gauche.
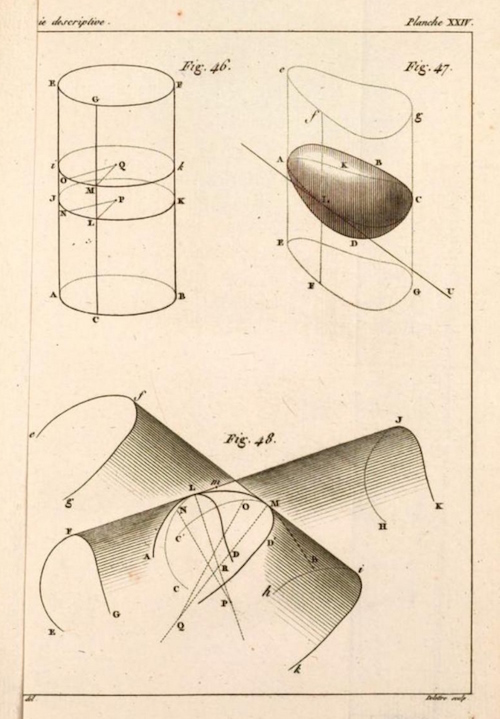
25 planches, 50 figures
-
Titre
-
Géométrie descriptive. Leçons données aux Écoles normales, l'an 3 de la République