Contenus
Classe
Document
Site
MathsInMetz
-
Gallica-Math: Répertoire Bibliographique des Sciences Mathématiques (1894-1912)Base de données;Publié de 1894 à 1912 par paquet de 1000 notices, le Répertoire Bibliographique des Sciences Mathématiques recense les publications significatives dans les domaines des mathématiques pures et appliquées faites à partir de 1800. De 2002 à 2009, la Bibliothèque nationale de France numérise le Répertoire Bibliographique des Sciences Mathématiques, élaboré de 1894 à 1912. Une collaboration est organisée avec la cellule Mathdoc de l'Université de Grenoble, pour les aspects informatiques, et avec les Archives Henri Poincaré pour les aspects historiques. Un site web dédié est créé. L'interface intègre de nos jours un ensemble de possibilités : moteur de recherche avancé, navigation à l'aide du code de classement, par nom de la revue. La base se montre particulièrement adaptée pour les études historiques portant sur la période 1800 à 1912.
-
Réquisitoire de M. le procureur général du parlement de Metz (et arrêt rendu sur icelui) au sujet des soi-disans JésuitesLivre; Lois et règlements; 1762; Humbert, Jean-Louis;Réquisitoire lancé par le Parlement de Metz, conduisant à la fermeture des collèges jésuites localisés dans les Trois-Évéchés à savoir Metz, Sedan et Verdun. L'arrêt est signé Humbert, collationné Brouet, imprimé par Joseph Collignon à Metz. Les collèges du Barrois et du Duché de Lorraine ne sont pas concernés.
-
Traité abrégé de physique à l'usage des collègesLivre; Cours de physique; 1763;
 Saintignon, Joseph de, Abbé (1716-1795);
En 1763, Saintignon publie en six tomes au format in-12 un "Traité abrégé de physique à l'usage des collèges" inspiré des leçons de l'Abbé Nollet, très littéraire dans sa forme. Après dédicace au Comte d'Estrée, alors Louis Charles César Le Tellier (1695-1771), les principes de physique connus et admis à cette époque sont exposés, y compris la gravité universelle de Newton. Pilâtre de Rozier a pu suivre dans ses jeunes années les cours professés par Saintignon au Collège Saint-Louis de Fort-Moselle, quartier dans lequel loge la famille. L'audience revendiquée est celle de collégiens, équivalent de nos jours à lycéen. Localisé à la bibliothèque de Polytechnique, l'exemplaire a été numérisé et rendu visible par la BnF. Les titres mis en avance par Saintignon sont " Procureur Général des Chanoines Réguliers de la Congrégation de Notre Sauveur, de la Société Royale des Sciences & des Arts de Metz, &c.".
Saintignon, Joseph de, Abbé (1716-1795);
En 1763, Saintignon publie en six tomes au format in-12 un "Traité abrégé de physique à l'usage des collèges" inspiré des leçons de l'Abbé Nollet, très littéraire dans sa forme. Après dédicace au Comte d'Estrée, alors Louis Charles César Le Tellier (1695-1771), les principes de physique connus et admis à cette époque sont exposés, y compris la gravité universelle de Newton. Pilâtre de Rozier a pu suivre dans ses jeunes années les cours professés par Saintignon au Collège Saint-Louis de Fort-Moselle, quartier dans lequel loge la famille. L'audience revendiquée est celle de collégiens, équivalent de nos jours à lycéen. Localisé à la bibliothèque de Polytechnique, l'exemplaire a été numérisé et rendu visible par la BnF. Les titres mis en avance par Saintignon sont " Procureur Général des Chanoines Réguliers de la Congrégation de Notre Sauveur, de la Société Royale des Sciences & des Arts de Metz, &c.". -
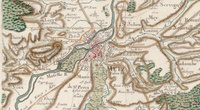 Carte générale de la France. 141, [Metz]. N°141. Flle 73 / [établie sous la direction de César-François Cassini de Thury]Carte géographique; 1763-1766; Cassini de Thury, César-François (1714-1784);
La feuille 141 résulte de l'assemblage de 21 gravures sur plaque de cuivre, élaborées sous la direction de César-François Cassini (1714-1784) et publiée vers 1766. Les villes principales qui figurent sur cette feuille sont au sud-ouest Ars-sur-Moselle, au nord-ouest Thionville; au nord-est Sarrelouis (alors territoire français jusqu'en 1815) et Sarrebruck, au sud-est Sarralbe. L'échelle est de 1/86400, avec une ligne pour cent toises. Un lavis appliqué à la main en sept couleurs permet de renforcer le rendu des reliefs obtenu à l'aide de hachures, d'indiquer les végétations et cours d'eaux. De nombreux textes complètent les indications graphiques. Localisée sur une frontière à protéger et fortifier, cette carte est l'une des première tracée. Comme tous les Cassini, César-François Cassini (1714-1784) habite le même appartement du premier étage de l'Observatoire de Paris, dont il deviendra le "Directeur général", avec trois mille livres de rente. Il obtiendra que ce droit devienne héréditaire. Ses travaux astronomiques que l'on retrouve dans les Mémoires de l'Académie des Sciences sont modestes et ne sont pas restés dans l'histoire des sciences. Cassini III (troisième de la dynastie) sera avant tout un géodésien-cartographe de grand talent. Sa carte de France est un des classiques du genre : il corrige la méridienne qui passe par l'Observatoire et devient chargé, sous Louis XV, de la description géométrique de la France. Le fruit de ses travaux sera cette carte de la France, composée de 180 feuilles, publiée au nom de l'Académie des sciences de 1744 à 1793, et qui offre la représentation la plus fidèle du pays, sur une échelle d'une ligne pour 100 toises. César Cassini ne pourra achever cette vaste entreprise, et son fils Jean-Dominique Cassini IV (1748-1845) sera chargé de la terminer, durant le début des années révolutionnaires.
Carte générale de la France. 141, [Metz]. N°141. Flle 73 / [établie sous la direction de César-François Cassini de Thury]Carte géographique; 1763-1766; Cassini de Thury, César-François (1714-1784);
La feuille 141 résulte de l'assemblage de 21 gravures sur plaque de cuivre, élaborées sous la direction de César-François Cassini (1714-1784) et publiée vers 1766. Les villes principales qui figurent sur cette feuille sont au sud-ouest Ars-sur-Moselle, au nord-ouest Thionville; au nord-est Sarrelouis (alors territoire français jusqu'en 1815) et Sarrebruck, au sud-est Sarralbe. L'échelle est de 1/86400, avec une ligne pour cent toises. Un lavis appliqué à la main en sept couleurs permet de renforcer le rendu des reliefs obtenu à l'aide de hachures, d'indiquer les végétations et cours d'eaux. De nombreux textes complètent les indications graphiques. Localisée sur une frontière à protéger et fortifier, cette carte est l'une des première tracée. Comme tous les Cassini, César-François Cassini (1714-1784) habite le même appartement du premier étage de l'Observatoire de Paris, dont il deviendra le "Directeur général", avec trois mille livres de rente. Il obtiendra que ce droit devienne héréditaire. Ses travaux astronomiques que l'on retrouve dans les Mémoires de l'Académie des Sciences sont modestes et ne sont pas restés dans l'histoire des sciences. Cassini III (troisième de la dynastie) sera avant tout un géodésien-cartographe de grand talent. Sa carte de France est un des classiques du genre : il corrige la méridienne qui passe par l'Observatoire et devient chargé, sous Louis XV, de la description géométrique de la France. Le fruit de ses travaux sera cette carte de la France, composée de 180 feuilles, publiée au nom de l'Académie des sciences de 1744 à 1793, et qui offre la représentation la plus fidèle du pays, sur une échelle d'une ligne pour 100 toises. César Cassini ne pourra achever cette vaste entreprise, et son fils Jean-Dominique Cassini IV (1748-1845) sera chargé de la terminer, durant le début des années révolutionnaires. -
Cours de mathématiques à l'usage des Gardes du pavillon et de la MarineLivre; Cours de mathématiques; Mathématiques appliquées; 1764-1770;
 Bézout, Étienne (1730-1783);
En 1764, le duc de Choiseul, ministre de la Marine, mène une politique de réforme. Sur recommandation de Charles-Étienne Camus et de l'abbé Nollet, il nomme Bézout examinateur des Gardes du Pavillon, avec charge de réformer l'enseignement en mathématique, physique et théorie d'élèves officiers de la Marine d'origine noble. Un cours est écrit dont le premier tome sur l'arithmétique parait en 1764. Une parution en quatre volumes est tout d'abord envisagée. "Le Cours de Mathématiques dont il s'agit ici, sera divisé en quatre Parties. La première traite de l'Arithmétique. La seconde traitera de la Géométrie dans laquelle on comprendra la Trigonométrie rectiligne & la Trigonométrie sphérique. La troisième aura pour objet, l'Algèbre & l'application de l’Algèbre à la Géométrie. La quatrième comprendra la Statique & le Mouvement, avec quelques propositions d'Hydrostatique & d'Hydraulique". Au final, un traité en six volumes in-8 avec planches est publié, paru entre 1764 et 1770 pour la première édition chez J.B.G. Musier. Plusieurs éditions se succèdent, du vivant de Bézout, et postérieurement à son décès survenu en 1783. Certaines parties deviennent traduites et adaptées en portugais et en anglais. Le cours comprend, avec certaines des dates de réédition: 1/ Première partie. Élémens d'arithmétique (1764, 1781); la version de 1781, établie du vivant de Bézout. Traduit et adapté en portugais et anglais, de 1785 à 1842; 2/ Seconde partie. Contenant les Élémens de Géométrie, la trigonométrie rectiligne, la trigonométrie sphérique (1765, 1779, 1810); adapté en anglais par John Farrar et publié de 1822 à 1837, pour enseignement à Harvard. 3/ Troisième partie. Contenant l'algèbre & l'application de cette science à l'arithmétique & à la géométrie (1766, 1775, 1797); adapté par Sylvestre Lacroix 4/ Quatrième partie. Contenant les principes généraux de la mécanique, précédés des principes de calcul qui servent d'introduction aux sciences physico-mathématiques (1767, 1770); 5/ Suite de la quatrième partie. Contenant l'application des principes généraux de la méchanique, à différents cas de mouvement & d'équilibre (1767, 1770, 1788). Les partie 4 et 5 sont liées. 6/ Suite du cours de mathématiques. Traité de navigation (1769, 1775, 1793, 1814). Possiblement indépendant. Traduit en portugais dès 1785 et publié jusqu'en 1820. Adapté en français par De Rossel en 1814. J.B.G. Musier fils à Paris (de 1764 à 1779) est le premier de plusieurs éditeurs du cours. Si le découpage pour la Marine est conservé, l'examen des rééditions posthumes montre que l'original est conservé de manière plus ou moins importante. En France de 1781 à 1789, l'éditeur Ph.D. PIERRES succède à Musier, puis en 1791, seul paraît "Versailles" en nom d"éditeur. Les éditeurs français sont ensuite, en 1798-1799 "Richard à Paris", suivi de F. Didot à Paris, de 1811 à 1822 pour les volumes 1 et 2 seulement (L. Alfonsi). Une série d'auteurs se saisissent du cours pour la Marine. Ils y apportent des notes et des ajouts. Parmi les plus importants, en terme de nombre d'exemplaires écoulés, il est possible de citer les noms de François Peyrard (1759-1822), de Jean Guillaume Garnier (1766-1840), d'Antoine André Louis Reynaud (1771-1844), de Sylvestre François Lacroix (1765_1843), tous contributeurs en relation avec l'École polytechnique, de 1795 à 1815 et ultérieurement. Le Traité de navigation (volume 6) devient adapté et publié de nouveau en 1814, chez Courcel, par Élisabeth-Paul-Édouard de Rossel (1765-1829). Cette version inclut notamment, sous forme de supplément, de nouvelles méthode de mesure de la longitude. La technique de la distance lunaire devient adoptée. De nouvelles tables nautiques sont publiées en ajout de la "Connaissance des temps". Le livre original de Bézout participe également à la politique de réforme de la Marine menée au Portugal. A partir de 1782 et jusqu'en 1824, certains volumes sont traduits sous le titre "Curso de Mathematicas para uso dos Guardas-Bandeiras e Guardas-Marinha" et professées dans les Universités de Coimbra et Lisbonne. Des versions remaniées des premiers volumes, notamment par Lacroix, deviennent traduits par John Farrar et publiés aux États-Unis, à partir de 1822 et jusqu'en 1836. Des livres d'Arithmétique, de Géométrie et d'Algèbre de Bézout et d'autres (Euler, Legendre, Lacroix), traduits et adaptés, deviennent utilisés pour les enseignements en plusieurs universités américaines, comme par exemple à Harvard, Massachusetts.
Bézout, Étienne (1730-1783);
En 1764, le duc de Choiseul, ministre de la Marine, mène une politique de réforme. Sur recommandation de Charles-Étienne Camus et de l'abbé Nollet, il nomme Bézout examinateur des Gardes du Pavillon, avec charge de réformer l'enseignement en mathématique, physique et théorie d'élèves officiers de la Marine d'origine noble. Un cours est écrit dont le premier tome sur l'arithmétique parait en 1764. Une parution en quatre volumes est tout d'abord envisagée. "Le Cours de Mathématiques dont il s'agit ici, sera divisé en quatre Parties. La première traite de l'Arithmétique. La seconde traitera de la Géométrie dans laquelle on comprendra la Trigonométrie rectiligne & la Trigonométrie sphérique. La troisième aura pour objet, l'Algèbre & l'application de l’Algèbre à la Géométrie. La quatrième comprendra la Statique & le Mouvement, avec quelques propositions d'Hydrostatique & d'Hydraulique". Au final, un traité en six volumes in-8 avec planches est publié, paru entre 1764 et 1770 pour la première édition chez J.B.G. Musier. Plusieurs éditions se succèdent, du vivant de Bézout, et postérieurement à son décès survenu en 1783. Certaines parties deviennent traduites et adaptées en portugais et en anglais. Le cours comprend, avec certaines des dates de réédition: 1/ Première partie. Élémens d'arithmétique (1764, 1781); la version de 1781, établie du vivant de Bézout. Traduit et adapté en portugais et anglais, de 1785 à 1842; 2/ Seconde partie. Contenant les Élémens de Géométrie, la trigonométrie rectiligne, la trigonométrie sphérique (1765, 1779, 1810); adapté en anglais par John Farrar et publié de 1822 à 1837, pour enseignement à Harvard. 3/ Troisième partie. Contenant l'algèbre & l'application de cette science à l'arithmétique & à la géométrie (1766, 1775, 1797); adapté par Sylvestre Lacroix 4/ Quatrième partie. Contenant les principes généraux de la mécanique, précédés des principes de calcul qui servent d'introduction aux sciences physico-mathématiques (1767, 1770); 5/ Suite de la quatrième partie. Contenant l'application des principes généraux de la méchanique, à différents cas de mouvement & d'équilibre (1767, 1770, 1788). Les partie 4 et 5 sont liées. 6/ Suite du cours de mathématiques. Traité de navigation (1769, 1775, 1793, 1814). Possiblement indépendant. Traduit en portugais dès 1785 et publié jusqu'en 1820. Adapté en français par De Rossel en 1814. J.B.G. Musier fils à Paris (de 1764 à 1779) est le premier de plusieurs éditeurs du cours. Si le découpage pour la Marine est conservé, l'examen des rééditions posthumes montre que l'original est conservé de manière plus ou moins importante. En France de 1781 à 1789, l'éditeur Ph.D. PIERRES succède à Musier, puis en 1791, seul paraît "Versailles" en nom d"éditeur. Les éditeurs français sont ensuite, en 1798-1799 "Richard à Paris", suivi de F. Didot à Paris, de 1811 à 1822 pour les volumes 1 et 2 seulement (L. Alfonsi). Une série d'auteurs se saisissent du cours pour la Marine. Ils y apportent des notes et des ajouts. Parmi les plus importants, en terme de nombre d'exemplaires écoulés, il est possible de citer les noms de François Peyrard (1759-1822), de Jean Guillaume Garnier (1766-1840), d'Antoine André Louis Reynaud (1771-1844), de Sylvestre François Lacroix (1765_1843), tous contributeurs en relation avec l'École polytechnique, de 1795 à 1815 et ultérieurement. Le Traité de navigation (volume 6) devient adapté et publié de nouveau en 1814, chez Courcel, par Élisabeth-Paul-Édouard de Rossel (1765-1829). Cette version inclut notamment, sous forme de supplément, de nouvelles méthode de mesure de la longitude. La technique de la distance lunaire devient adoptée. De nouvelles tables nautiques sont publiées en ajout de la "Connaissance des temps". Le livre original de Bézout participe également à la politique de réforme de la Marine menée au Portugal. A partir de 1782 et jusqu'en 1824, certains volumes sont traduits sous le titre "Curso de Mathematicas para uso dos Guardas-Bandeiras e Guardas-Marinha" et professées dans les Universités de Coimbra et Lisbonne. Des versions remaniées des premiers volumes, notamment par Lacroix, deviennent traduits par John Farrar et publiés aux États-Unis, à partir de 1822 et jusqu'en 1836. Des livres d'Arithmétique, de Géométrie et d'Algèbre de Bézout et d'autres (Euler, Legendre, Lacroix), traduits et adaptés, deviennent utilisés pour les enseignements en plusieurs universités américaines, comme par exemple à Harvard, Massachusetts. -
 I. Cours de mathématiques à l'usage des Gardes du pavillon et de la Marine. Première partie. Élémens d'arithmétiqueLivre; Cours d'arithmétique; 1764; 1781; 1798; 1824; 1848;
I. Cours de mathématiques à l'usage des Gardes du pavillon et de la Marine. Première partie. Élémens d'arithmétiqueLivre; Cours d'arithmétique; 1764; 1781; 1798; 1824; 1848;  Bézout, Étienne (1730-1783);
1764. Paris: J.B.G. Musier. non numérisé 1781. Paris: Ph.D. Pierres. 256 pages. 246 leçons 1798. Paris: Firmin Didot. 258 pages. 267 leçons Ce cours est fusionné par Bézout avec celui de géométrie en 1770 pour donner lieu à la première partie du premier volume du cours à l'usage du Corps royal de l'Artillerie. Bézout meurt en 1783, mais certains de ses cours dont celui d'arithmétique restent demandés et sont réédités plusieurs fois jusqu'en 1833. En 1798 an VII, l'arithmétique subit une évolution notable sous la plume de François Peyrard (1759-1822). De 1795 à 1804, ce dernier, directeur de la bibliothèque de l'École polytechnique, complète l'ouvrage à l'aide d'un "Tableau des principales monnaies étrangères" et d'un "Tableau des poids et mesures des Pays étrangers". En 1821, Antoine André Louis Reynaud (1771-1844), examinateur à l'École polytechnique, publie chez Mme Vve Courcier, l'éditrice parisienne spécialisée en livres de mathématiques, la neuvième édition officielle de l'arithmétique de Bézout, en 152 pages, 246 leçons, complétées de notes. Reynaud souligne l'application du cours aux usages dans l'artillerie et la marine, l'arpentage et le commerce. Les tables qui complètent l'ouvrage sont : Tableaux de conversion entre anciennes et nouvelles mesures (distance, longueur, superficie, volume, poids); Comparaison des monnaies (nouvelles, anciennes, étrangères);Table des logarithmes de 1 à 10000. En 1824, la première traduction en anglais à destination du public américain est due à Nathaniel Haynes A. B., tuteur en mathématiques au Gardiner Lyceum, à Gardiner, Maine. Le traducteur souligne l'adoption du livre en France par l'École polytechnique. Un autre traducteur américain de Bézout, John Farrar, va promouvoir un enseignement adapté. En France, des versions assez éloignées du livre original circulent en 1848. Caillet P.H. entreprend alors une édition basée sur le texte original de 1781, sans modification autre que l'introduction du système métrique et l'application du calcul aux monnaies et mesures des pays étrangers. Le livre devient intégré à la liste officielle des ouvrages autorisés par le ministère dans les écoles normales primaires.
Bézout, Étienne (1730-1783);
1764. Paris: J.B.G. Musier. non numérisé 1781. Paris: Ph.D. Pierres. 256 pages. 246 leçons 1798. Paris: Firmin Didot. 258 pages. 267 leçons Ce cours est fusionné par Bézout avec celui de géométrie en 1770 pour donner lieu à la première partie du premier volume du cours à l'usage du Corps royal de l'Artillerie. Bézout meurt en 1783, mais certains de ses cours dont celui d'arithmétique restent demandés et sont réédités plusieurs fois jusqu'en 1833. En 1798 an VII, l'arithmétique subit une évolution notable sous la plume de François Peyrard (1759-1822). De 1795 à 1804, ce dernier, directeur de la bibliothèque de l'École polytechnique, complète l'ouvrage à l'aide d'un "Tableau des principales monnaies étrangères" et d'un "Tableau des poids et mesures des Pays étrangers". En 1821, Antoine André Louis Reynaud (1771-1844), examinateur à l'École polytechnique, publie chez Mme Vve Courcier, l'éditrice parisienne spécialisée en livres de mathématiques, la neuvième édition officielle de l'arithmétique de Bézout, en 152 pages, 246 leçons, complétées de notes. Reynaud souligne l'application du cours aux usages dans l'artillerie et la marine, l'arpentage et le commerce. Les tables qui complètent l'ouvrage sont : Tableaux de conversion entre anciennes et nouvelles mesures (distance, longueur, superficie, volume, poids); Comparaison des monnaies (nouvelles, anciennes, étrangères);Table des logarithmes de 1 à 10000. En 1824, la première traduction en anglais à destination du public américain est due à Nathaniel Haynes A. B., tuteur en mathématiques au Gardiner Lyceum, à Gardiner, Maine. Le traducteur souligne l'adoption du livre en France par l'École polytechnique. Un autre traducteur américain de Bézout, John Farrar, va promouvoir un enseignement adapté. En France, des versions assez éloignées du livre original circulent en 1848. Caillet P.H. entreprend alors une édition basée sur le texte original de 1781, sans modification autre que l'introduction du système métrique et l'application du calcul aux monnaies et mesures des pays étrangers. Le livre devient intégré à la liste officielle des ouvrages autorisés par le ministère dans les écoles normales primaires. -
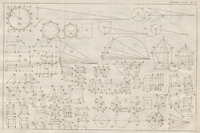 II. Cours de mathématiques à l'usage des Gardes du pavillon et de la Marine. Seconde partie, contenant les Éléments de géométrie, la Trigonométrie rectiligne & la Trigonométrie sphériqueLivre; Cours de géométrie; Cours de trigonométrie; 1765; 1779; 1782; 1833;
II. Cours de mathématiques à l'usage des Gardes du pavillon et de la Marine. Seconde partie, contenant les Éléments de géométrie, la Trigonométrie rectiligne & la Trigonométrie sphériqueLivre; Cours de géométrie; Cours de trigonométrie; 1765; 1779; 1782; 1833;  Bézout, Étienne (1730-1783);
1779. Paris : J. B. G. Musier. 357 pages. 7 planches, 184 figures. 362 leçons. 1782. Paris : Ph-D Pierres. 356 pages. 7 planches, 184 figures. 361 leçons. 1833. Boston : Hilliard, Gray. 165 pages. 183 leçons. Publié avant la Révolution chez Musier, l'intérêt pour la géométrie et les deux trigonométries pour la Marine se montre renouvelé postérieurement à la Révolution, avec des adaptations de plusieurs auteurs comme Silvestre François Lacroix (1779–1843) et d'autres. En 1833, le cours de Bézout sur les trigonométries planes et sphériques devient adapté et compilé. Considérablement remanié, il est traduit en anglais parJohn Farrar (1779-1853) "An Elementary Treatise on Plane and Spherical Trigonometry, and on the Application of Algebra to Geometry" et publié plusieurs fois, en 1822, 1826, 1833, 1837 notamment. Le cours devient enseigné, notamment à Harvard; la version numérisée provient de l'UCLA.
Bézout, Étienne (1730-1783);
1779. Paris : J. B. G. Musier. 357 pages. 7 planches, 184 figures. 362 leçons. 1782. Paris : Ph-D Pierres. 356 pages. 7 planches, 184 figures. 361 leçons. 1833. Boston : Hilliard, Gray. 165 pages. 183 leçons. Publié avant la Révolution chez Musier, l'intérêt pour la géométrie et les deux trigonométries pour la Marine se montre renouvelé postérieurement à la Révolution, avec des adaptations de plusieurs auteurs comme Silvestre François Lacroix (1779–1843) et d'autres. En 1833, le cours de Bézout sur les trigonométries planes et sphériques devient adapté et compilé. Considérablement remanié, il est traduit en anglais parJohn Farrar (1779-1853) "An Elementary Treatise on Plane and Spherical Trigonometry, and on the Application of Algebra to Geometry" et publié plusieurs fois, en 1822, 1826, 1833, 1837 notamment. Le cours devient enseigné, notamment à Harvard; la version numérisée provient de l'UCLA. -
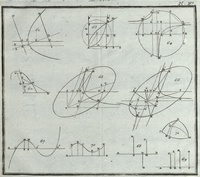 III. Cours de mathématiques à l'usage des Gardes du pavillon et de la Marine. Troisième partie. Contenant l'Algèbre & l'application de cette science à l'Arithmétique & à la Géométrie.Livre; Cours d'algèbre; 1766; 1781;
III. Cours de mathématiques à l'usage des Gardes du pavillon et de la Marine. Troisième partie. Contenant l'Algèbre & l'application de cette science à l'Arithmétique & à la Géométrie.Livre; Cours d'algèbre; 1766; 1781;  Bézout, Étienne (1730-1783);
1781, In-8, 488 pages, 4 planches, 419 leçons
Bézout, Étienne (1730-1783);
1781, In-8, 488 pages, 4 planches, 419 leçons -
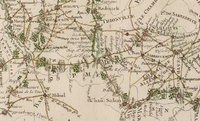 L'indicateur fidèle du voyageur, Metz et son réseau routierCarte routière; 1767;
Les "indicateurs fidèles du voyageur" constituent des atlas routiers fréquemment édités sous l'Ancien régime. Ils existent en deux formats, de poche et in-quarto pour le bureau. Dans les versions de luxe, les cartes sont colorées à la main, pour mieux faire ressortir les villes, postes, chemins et paysages rencontrés. Les distances, heure de départ, temps de parcours entre villes et relais, ville de dinée et couchée sont mentionnés. Les unités de distance sont les lieues (petite lieue, lieue commune, grande lieue). Des hachures mentionnent les côtes et descentes de la route. Les routes royales, mieux entretenues, sont marquées de chaque côté de pointillés symbolisant les arbres plantés de part et d'autre de la voie. En 1767, on se rend en carrosse de Paris à Metz (68L) en 4 jours, en faisant halte à Verdun le troisième jour. On va de Paris à Strasbourg en 12 jours, en faisant étape à Nancy le huitième jour. A partir de 1780, avec la diligence et du fait de l'amélioration des chaussées, on se rend de Paris à Strasbourg en 4,5 jours, en parcourant des étapes de plus de 100 kilomètres. Construite par Vauban et française jusqu'en 1815, la forteresse de Sarrelouis se trouve bien desservie depuis Metz. Instituée de 1738 à 1787, l'impopulaire corvée royale permet l'entretien des routes. En ce qui concerne les inspections, l'instruction du 13 mai 1754 du garde des sceaux, contrôleur général, détermine les fonctions du premier ingénieur, des quatre inspecteurs généraux des ponts et chaussées, des vingt-huit ingénieurs, des cent trois sous-ingénieurs et des quarante-quatre élèves ou conducteurs principaux. Le premier département d'inspection dont dépend la Lorraine, en résidence à Paris, intègre Le Hainaut, les généralités d'Amiens, Soissons, Châlons, Metz et Paris. Créée lors de la Révolution, l'École centrale des travaux publics prend le nom d'École polytechnique par le décret du 15 fructidor an III (1er septembre 1795). L'École nationale des ponts et chaussées devient alors un établissement d'application de l'École polytechnique. Le corps des ingénieurs des ponts et chaussées propose une carrière complète, assurée par le gouvernement.
L'indicateur fidèle du voyageur, Metz et son réseau routierCarte routière; 1767;
Les "indicateurs fidèles du voyageur" constituent des atlas routiers fréquemment édités sous l'Ancien régime. Ils existent en deux formats, de poche et in-quarto pour le bureau. Dans les versions de luxe, les cartes sont colorées à la main, pour mieux faire ressortir les villes, postes, chemins et paysages rencontrés. Les distances, heure de départ, temps de parcours entre villes et relais, ville de dinée et couchée sont mentionnés. Les unités de distance sont les lieues (petite lieue, lieue commune, grande lieue). Des hachures mentionnent les côtes et descentes de la route. Les routes royales, mieux entretenues, sont marquées de chaque côté de pointillés symbolisant les arbres plantés de part et d'autre de la voie. En 1767, on se rend en carrosse de Paris à Metz (68L) en 4 jours, en faisant halte à Verdun le troisième jour. On va de Paris à Strasbourg en 12 jours, en faisant étape à Nancy le huitième jour. A partir de 1780, avec la diligence et du fait de l'amélioration des chaussées, on se rend de Paris à Strasbourg en 4,5 jours, en parcourant des étapes de plus de 100 kilomètres. Construite par Vauban et française jusqu'en 1815, la forteresse de Sarrelouis se trouve bien desservie depuis Metz. Instituée de 1738 à 1787, l'impopulaire corvée royale permet l'entretien des routes. En ce qui concerne les inspections, l'instruction du 13 mai 1754 du garde des sceaux, contrôleur général, détermine les fonctions du premier ingénieur, des quatre inspecteurs généraux des ponts et chaussées, des vingt-huit ingénieurs, des cent trois sous-ingénieurs et des quarante-quatre élèves ou conducteurs principaux. Le premier département d'inspection dont dépend la Lorraine, en résidence à Paris, intègre Le Hainaut, les généralités d'Amiens, Soissons, Châlons, Metz et Paris. Créée lors de la Révolution, l'École centrale des travaux publics prend le nom d'École polytechnique par le décret du 15 fructidor an III (1er septembre 1795). L'École nationale des ponts et chaussées devient alors un établissement d'application de l'École polytechnique. Le corps des ingénieurs des ponts et chaussées propose une carrière complète, assurée par le gouvernement. -
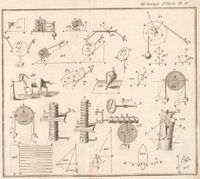 V. Cours de mathématiques à l'usage des Gardes du Pavillon et de la Marine. Suite de la quatrième partie. Contenant l'Application des principes généraux de la Méchanique à différents cas de mouvement & d'équilibreLivre; Cours de mécanique; 1767; 1770; 1772; 1777; 1788;
V. Cours de mathématiques à l'usage des Gardes du Pavillon et de la Marine. Suite de la quatrième partie. Contenant l'Application des principes généraux de la Méchanique à différents cas de mouvement & d'équilibreLivre; Cours de mécanique; 1767; 1770; 1772; 1777; 1788;  Bézout, Étienne (1730-1783);
1767. Paris. JBG Musier, 467 pages, 11 planches, 203 figures, pas de table des matières 1770. Paris. JBG Musier, 479 pages, 11 planches, 203 figures, pas de table de données, table des matières, leçons 376 à 735 1772. Paris. JBG Musier, non numérisé, 1788. Paris. PH.-D. PIERRES, 480 pages, 13 planches, 128 figures, 8 tables de données, leçons 350 à 854,
Bézout, Étienne (1730-1783);
1767. Paris. JBG Musier, 467 pages, 11 planches, 203 figures, pas de table des matières 1770. Paris. JBG Musier, 479 pages, 11 planches, 203 figures, pas de table de données, table des matières, leçons 376 à 735 1772. Paris. JBG Musier, non numérisé, 1788. Paris. PH.-D. PIERRES, 480 pages, 13 planches, 128 figures, 8 tables de données, leçons 350 à 854, -
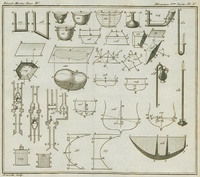 IV. Cours de mathématiques à l'usage des Gardes du Pavillon et de la Marine. Quatrième partie. Contenant les Principes généraux de la Mécanique, précédés des Principes de calcul qui servent d'introduction aux Sciences physico-mathématiquesLivre; Cours d'algèbre; Cours de mécanique; 1767; 1770; 1799;
IV. Cours de mathématiques à l'usage des Gardes du Pavillon et de la Marine. Quatrième partie. Contenant les Principes généraux de la Mécanique, précédés des Principes de calcul qui servent d'introduction aux Sciences physico-mathématiquesLivre; Cours d'algèbre; Cours de mécanique; 1767; 1770; 1799;  Bézout, Étienne (1730-1783);
1767. n'a pas été retrouvée numérisée. 1770. à Paris, J.B.G. Musier, 432 pages, leçons 1 à 375, 5 planches d'illustrations. - Cours de calcul différentiel et intégral. pages 1-231, leçons de 1 à 178. - Première partie du Cours de mécanique physique. pages 232-432, leçons 180 à 375.
Bézout, Étienne (1730-1783);
1767. n'a pas été retrouvée numérisée. 1770. à Paris, J.B.G. Musier, 432 pages, leçons 1 à 375, 5 planches d'illustrations. - Cours de calcul différentiel et intégral. pages 1-231, leçons de 1 à 178. - Première partie du Cours de mécanique physique. pages 232-432, leçons 180 à 375. -
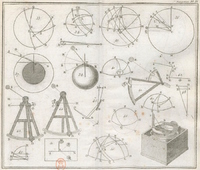 VI. Suite du cours de mathématiques à l'usage des Gardes du pavillon et de la Marine. Contenant le Traité de navigation.Livre; Cours de navigation; Cours d'astronomie; 1769; 1775; 1793; 1785; 1814;
VI. Suite du cours de mathématiques à l'usage des Gardes du pavillon et de la Marine. Contenant le Traité de navigation.Livre; Cours de navigation; Cours d'astronomie; 1769; 1775; 1793; 1785; 1814;  Bézout, Étienne (1730-1783);
Le Traité de Navigation de Bézout est successivement édité chez plusieurs imprimeurs-libraires : 1/ Paris : J.B.G. Musier fils, Libraire, quai des Augustins, à S. Etienne. (1769, 1775, 1793). 319 pages. 20 tableaux. 10 planches, 69 figures. 2/ Paris : J.B.G. Musier fils, Libraire, quai des Augustins, à S. Etienne. 1775. 319 pages. 20 tableaux. 10 planches, 69 figures. 3/ Paris : PH. D. Pierres. rue St. -Jacques. 1793. 296 pages. 20 tableaux. 10 planches, 69 figures. En 1785, le cours devient traduit en portugais sous le titre "Curso de mathematica para uso dos guardas-bandeiras e guardas-marinha : que contem o tratado de navegação", 316 pages, 10 planches, 69 figures. Diffusé au Brésil également. Puis De Rossel adapte le cours en 1814, pour intégrer dans un section supplémentaire les nouvelles méthodes de calcul des longitudes. En effet, avec Lalande à partir de 1772, la "Connaissance des temps" passe d’une éphéméride au seul usage des astronomes, à un usage nautique avec la publication de tables des distances lunaires (observation des distances angulaires entre la Lune et le Soleil ou la Lune et des étoiles choisies du zodiaque), méthode reine pour la détermination des «longitudes à la mer», jusqu’en 1905. La technique apporte des simplifications dans les mesures astrales et les calculs. Le livre devient alors diffusé chez Courcier, libraire parisien phare des années 1810 à 1830 pour la diffusion des mathématiques pures et appliquées. Paris : Mme Ve Courcier, Imprim.-Lib., pour les Mathématiques et la Marine, quai des Augustins, n° 57. 1814. Bézout, De Rossel. 338 pages. 34 tableaux. 10 planches, 69 figures.
Bézout, Étienne (1730-1783);
Le Traité de Navigation de Bézout est successivement édité chez plusieurs imprimeurs-libraires : 1/ Paris : J.B.G. Musier fils, Libraire, quai des Augustins, à S. Etienne. (1769, 1775, 1793). 319 pages. 20 tableaux. 10 planches, 69 figures. 2/ Paris : J.B.G. Musier fils, Libraire, quai des Augustins, à S. Etienne. 1775. 319 pages. 20 tableaux. 10 planches, 69 figures. 3/ Paris : PH. D. Pierres. rue St. -Jacques. 1793. 296 pages. 20 tableaux. 10 planches, 69 figures. En 1785, le cours devient traduit en portugais sous le titre "Curso de mathematica para uso dos guardas-bandeiras e guardas-marinha : que contem o tratado de navegação", 316 pages, 10 planches, 69 figures. Diffusé au Brésil également. Puis De Rossel adapte le cours en 1814, pour intégrer dans un section supplémentaire les nouvelles méthodes de calcul des longitudes. En effet, avec Lalande à partir de 1772, la "Connaissance des temps" passe d’une éphéméride au seul usage des astronomes, à un usage nautique avec la publication de tables des distances lunaires (observation des distances angulaires entre la Lune et le Soleil ou la Lune et des étoiles choisies du zodiaque), méthode reine pour la détermination des «longitudes à la mer», jusqu’en 1905. La technique apporte des simplifications dans les mesures astrales et les calculs. Le livre devient alors diffusé chez Courcier, libraire parisien phare des années 1810 à 1830 pour la diffusion des mathématiques pures et appliquées. Paris : Mme Ve Courcier, Imprim.-Lib., pour les Mathématiques et la Marine, quai des Augustins, n° 57. 1814. Bézout, De Rossel. 338 pages. 34 tableaux. 10 planches, 69 figures. -
 Cours de Mathématiques à l'usage du Corps royal de l'ArtillerieLivre; Cours de mathématiques; 1770-1772;
Cours de Mathématiques à l'usage du Corps royal de l'ArtillerieLivre; Cours de mathématiques; 1770-1772;  Bézout, Étienne (1730-1783);
A l'usage des élèves officiers de l'artillerie, la première édition du cours de Bézout est publiée en quatre volumes, de 1770 à 1772, avec respectivement 6, 3, 6 et 13 planches dépliantes. Il s'agit d'une adaptation du cours pour la Marine publié précédemment, entre 1764 et 1770. Cette version pour l'artillerie va rencontrer un large succès, lié en partie au fait que le premier et le second tome (arithmétique, géométrie, algèbre) servent aussi à évaluer les candidats au concours d'entrée aux écoles militaires et à l'école polytechnique. Le cours pour l'artillerie devient une référence et d'autres éditions suivent. Simplifiées pour certaines, elles incluent les nouvelles unités de poids et de mesure, les monnaies de différents pays. 1/ Tome premier, "Contenant l’Arithmétique, la Géométrie & la Trigonométrie rectiligne" est une version abrégée en deux parties des tomes 1 et 2 du cours pour la Marine. La trigonométrie sphérique n'a pas été reprise. (1770, 1795 an III, 1797 an V, 1800 an VIII). 2/ Tome second, "Contenant l’Algèbre & l'application de l'Algèbre à la Géométrie" est une version abrégée du troisième cours aux gardes de la Marine. (1770) 3/ Tome troisième, "Principes Généraux de la Méchanique et de l'Hydrostatique, précédés des Principes du Calcul qui servent d'introduction aux Sciences Physico-Mathématiques" (1772) 4/ Tome quatrième, "Contenant l'application des principes généraux de la mécanique, à différents cas de mouvement et d'équilibre." Contient les résultats de certaines des recherches de Bézout (1772). Les éditeurs successifs français comprennent : Paris, Imprimerie royale pour la première édition (1770, 1772). Ph.-D- Pierres, imprimeur ordinaire du Roi, rue Saint-Jacques, pour la seconde (1780, 1781, 1782) et partiellement la troisième édition (an III 1794, an IV). Chez RICHARD, CAILLE & RAVIER, Libraires, rue Haute-Feuille , N°, 11 , au coin de la rue Serpente (quatrième partie AN VII) et d'autres. En 1785, Napoléon en étude à l'École militaire supérieure de Paris se distingue en maîtrisant en dix mois le cours de Bézout pour l'artillerie, étudié habituellement en trois ans. Du vivant de Bézout, le livre est adapté et traduit en allemand, en une version simplifiée en un seul volume : "Ueber die Kugel-Bahn, des Herrn Bezout : Nebst I. Kupfertafel" (Sur la trajectoire du boulet, par Monsieur Bézout, avec une gravure), Francfort 1782.
Bézout, Étienne (1730-1783);
A l'usage des élèves officiers de l'artillerie, la première édition du cours de Bézout est publiée en quatre volumes, de 1770 à 1772, avec respectivement 6, 3, 6 et 13 planches dépliantes. Il s'agit d'une adaptation du cours pour la Marine publié précédemment, entre 1764 et 1770. Cette version pour l'artillerie va rencontrer un large succès, lié en partie au fait que le premier et le second tome (arithmétique, géométrie, algèbre) servent aussi à évaluer les candidats au concours d'entrée aux écoles militaires et à l'école polytechnique. Le cours pour l'artillerie devient une référence et d'autres éditions suivent. Simplifiées pour certaines, elles incluent les nouvelles unités de poids et de mesure, les monnaies de différents pays. 1/ Tome premier, "Contenant l’Arithmétique, la Géométrie & la Trigonométrie rectiligne" est une version abrégée en deux parties des tomes 1 et 2 du cours pour la Marine. La trigonométrie sphérique n'a pas été reprise. (1770, 1795 an III, 1797 an V, 1800 an VIII). 2/ Tome second, "Contenant l’Algèbre & l'application de l'Algèbre à la Géométrie" est une version abrégée du troisième cours aux gardes de la Marine. (1770) 3/ Tome troisième, "Principes Généraux de la Méchanique et de l'Hydrostatique, précédés des Principes du Calcul qui servent d'introduction aux Sciences Physico-Mathématiques" (1772) 4/ Tome quatrième, "Contenant l'application des principes généraux de la mécanique, à différents cas de mouvement et d'équilibre." Contient les résultats de certaines des recherches de Bézout (1772). Les éditeurs successifs français comprennent : Paris, Imprimerie royale pour la première édition (1770, 1772). Ph.-D- Pierres, imprimeur ordinaire du Roi, rue Saint-Jacques, pour la seconde (1780, 1781, 1782) et partiellement la troisième édition (an III 1794, an IV). Chez RICHARD, CAILLE & RAVIER, Libraires, rue Haute-Feuille , N°, 11 , au coin de la rue Serpente (quatrième partie AN VII) et d'autres. En 1785, Napoléon en étude à l'École militaire supérieure de Paris se distingue en maîtrisant en dix mois le cours de Bézout pour l'artillerie, étudié habituellement en trois ans. Du vivant de Bézout, le livre est adapté et traduit en allemand, en une version simplifiée en un seul volume : "Ueber die Kugel-Bahn, des Herrn Bezout : Nebst I. Kupfertafel" (Sur la trajectoire du boulet, par Monsieur Bézout, avec une gravure), Francfort 1782. -
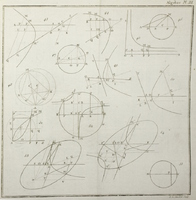 II. Cours de mathématiques, À l'usage du Corps royal de l'Artillerie. Tome second. Contenant l’Algèbre & l'Application de l'algèbre à la géométrieLivre; Cours d'algèbre; Cours de géométrie; 1770; 1781; 1797;
II. Cours de mathématiques, À l'usage du Corps royal de l'Artillerie. Tome second. Contenant l’Algèbre & l'Application de l'algèbre à la géométrieLivre; Cours d'algèbre; Cours de géométrie; 1770; 1781; 1797;  Bézout, Étienne (1730-1783);
1781. Ph,-D, PIERRES, 1781, 316 pages. 3 planches, 55 figures. Leçons 1 à 340.
Bézout, Étienne (1730-1783);
1781. Ph,-D, PIERRES, 1781, 316 pages. 3 planches, 55 figures. Leçons 1 à 340. -
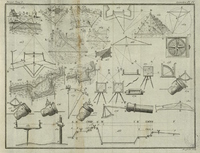 I. Cours de Mathématiques, À l'usage du Corps royal de l'Artillerie. Tome premier. Contenant l’Arithmétique, la Géométrie & la Trigonométrie rectiligneLivre; Cours d'arithmétique; Cours de géométrie; Cours de trigonométrie; 1770; 1795, an III; 1797, an V; 1800, an VIII;
I. Cours de Mathématiques, À l'usage du Corps royal de l'Artillerie. Tome premier. Contenant l’Arithmétique, la Géométrie & la Trigonométrie rectiligneLivre; Cours d'arithmétique; Cours de géométrie; Cours de trigonométrie; 1770; 1795, an III; 1797, an V; 1800, an VIII;  Bézout, Étienne (1730-1783);
Le premier volume du livre de Bézout pour l'artillerie sert à évaluer de manière orale et publique les élèves candidats au concours d'admission aux écoles d'officiers de l'artillerie et du génie. Les autres volumes sont étudiés par les élèves au cours de leur formation. Lors de sa carrière d'examinateur des candidats pour la marine puis l'artillerie (1764-1783), Bézout soutenu par Gribeauval (1715-1789) donne aux professeurs de mathématiques des instructions strictes sur les parties de ses livres à étudier, sur les emplois du temps à observer. Il examine personnellement les candidats et se rend notamment à Metz, jusqu'en 1783, année de son décès. Son poste d'examinateur des candidats à l'Artillerie est ensuite repris par Laplace jusqu'en 1793, mais le cours de Bézout reste cependant la référence. Dans la géométrie de Bézout, les postulats d'Euclide, jugés trop théoriques, ne sont pas enseignés. Sa géométrie se montre essentiellement appliquée à l'artillerie (la trigonométrie sphérique n'est pas enseignée), à l'architecture des fortifications et aux levers de terrains (cartographie à petite échelle des fortifications).
Bézout, Étienne (1730-1783);
Le premier volume du livre de Bézout pour l'artillerie sert à évaluer de manière orale et publique les élèves candidats au concours d'admission aux écoles d'officiers de l'artillerie et du génie. Les autres volumes sont étudiés par les élèves au cours de leur formation. Lors de sa carrière d'examinateur des candidats pour la marine puis l'artillerie (1764-1783), Bézout soutenu par Gribeauval (1715-1789) donne aux professeurs de mathématiques des instructions strictes sur les parties de ses livres à étudier, sur les emplois du temps à observer. Il examine personnellement les candidats et se rend notamment à Metz, jusqu'en 1783, année de son décès. Son poste d'examinateur des candidats à l'Artillerie est ensuite repris par Laplace jusqu'en 1793, mais le cours de Bézout reste cependant la référence. Dans la géométrie de Bézout, les postulats d'Euclide, jugés trop théoriques, ne sont pas enseignés. Sa géométrie se montre essentiellement appliquée à l'artillerie (la trigonométrie sphérique n'est pas enseignée), à l'architecture des fortifications et aux levers de terrains (cartographie à petite échelle des fortifications). -
 Cours de mathématiques à l'usage du Collège de MetzLivre; Cours d'arithmétique; Cours de géométrie; Cours de mathématiques; 1772-1773; Casbois, Nicolas (1728-1795, dom);
Cours de mathématiques à l'usage des élèves du Collège Saint-Symphorien, dispensé par le dominicain Casbois au collège rue de la Chèvre sous l'Ancien Régime. Publié en deux volumes chez Joseph Antoine à Metz. Volume 1. Arithmétique. 1772. 272 pages. Volume 2. Géométrie. 1773. 296 pages, 8 planches dépliantes. Non numérisé.
Cours de mathématiques à l'usage du Collège de MetzLivre; Cours d'arithmétique; Cours de géométrie; Cours de mathématiques; 1772-1773; Casbois, Nicolas (1728-1795, dom);
Cours de mathématiques à l'usage des élèves du Collège Saint-Symphorien, dispensé par le dominicain Casbois au collège rue de la Chèvre sous l'Ancien Régime. Publié en deux volumes chez Joseph Antoine à Metz. Volume 1. Arithmétique. 1772. 272 pages. Volume 2. Géométrie. 1773. 296 pages, 8 planches dépliantes. Non numérisé. -
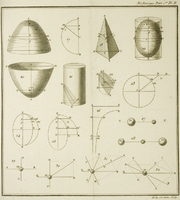 III. Cours de Mathématiques à l'usage du Corps royal de l'Artillerie. Tome troisième. Contenant les Principes généraux de la Mécanique et l'Hydrostatique. Précédés des Principes de calcul qui servent d'introduction aux Sciences physico-mathématiquesLivre; Cours d'analyse; Cours de mécanique; 1772; 1788; 1799;
III. Cours de Mathématiques à l'usage du Corps royal de l'Artillerie. Tome troisième. Contenant les Principes généraux de la Mécanique et l'Hydrostatique. Précédés des Principes de calcul qui servent d'introduction aux Sciences physico-mathématiquesLivre; Cours d'analyse; Cours de mécanique; 1772; 1788; 1799;  Bézout, Étienne (1730-1783);
1772. Paris. Imprim. royale. 381 pages. 6 planches 174 figures. Leçons 1 à 349 1788. Paris. Ph.D. Pierres. 381 pages. 6 planches. Leçons 1 à 349 1799 an VII. Paris. Richard, Cailles, Ravier, 368 pages. 4 planches, 69 figures. Leçons 1 à 349
Bézout, Étienne (1730-1783);
1772. Paris. Imprim. royale. 381 pages. 6 planches 174 figures. Leçons 1 à 349 1788. Paris. Ph.D. Pierres. 381 pages. 6 planches. Leçons 1 à 349 1799 an VII. Paris. Richard, Cailles, Ravier, 368 pages. 4 planches, 69 figures. Leçons 1 à 349 -
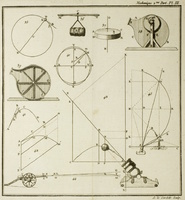 IV. Cours de mathématiques à l'usage du Corps royal de l'Artillerie. Tome quatrième. Contenant l'application des principes généraux de la mécanique, à différents cas de mouvement et d'équilibre.Livre; Cours de mécanique; 1772; 1788; 1801, an VIII;
IV. Cours de mathématiques à l'usage du Corps royal de l'Artillerie. Tome quatrième. Contenant l'application des principes généraux de la mécanique, à différents cas de mouvement et d'équilibre.Livre; Cours de mécanique; 1772; 1788; 1801, an VIII;  Bézout, Étienne (1730-1783);
1772. Impr. royale. 469 pages. 13 planches, 177 figures, 7 tableaux 1788. Ph.D. Pierres. 480 pages. 13 planches 1801 An VIII. Courcier. 488 pages. 5 planches
Bézout, Étienne (1730-1783);
1772. Impr. royale. 469 pages. 13 planches, 177 figures, 7 tableaux 1788. Ph.D. Pierres. 480 pages. 13 planches 1801 An VIII. Courcier. 488 pages. 5 planches -
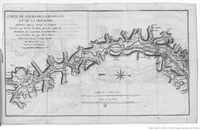 Mémoires concernant la navigation des rivières de la province des Trois-Évêchés et le commerce de la ville de Metz, lus dans l'assemblée publique de la Société royale des sciences et arts de Metz, tenue le 18 novembre 1772Livre collectif; Carte fluviale; 1773; Gardeur-Lebrun, Louis (1714-1786); Calonne, Charles-Alexandre de (1734-1802); Blouet, Jean-François-Nicolas (1745-1809); Mathis;
Carte fluviale de la Moselle entre Nancy et Coblence. Indications sur les difficultés de navigation et sur les taxes perçues lors des passages. In-4°, 424 pages. 4 planches. Échelles en toises et minutes. Livre collectif et carte. Gravure de Nicolas Chalmandrier, graveur parisien, également auteur de la carte du Canal royal de la province de Languedoc (Canal du Midi).
Mémoires concernant la navigation des rivières de la province des Trois-Évêchés et le commerce de la ville de Metz, lus dans l'assemblée publique de la Société royale des sciences et arts de Metz, tenue le 18 novembre 1772Livre collectif; Carte fluviale; 1773; Gardeur-Lebrun, Louis (1714-1786); Calonne, Charles-Alexandre de (1734-1802); Blouet, Jean-François-Nicolas (1745-1809); Mathis;
Carte fluviale de la Moselle entre Nancy et Coblence. Indications sur les difficultés de navigation et sur les taxes perçues lors des passages. In-4°, 424 pages. 4 planches. Échelles en toises et minutes. Livre collectif et carte. Gravure de Nicolas Chalmandrier, graveur parisien, également auteur de la carte du Canal royal de la province de Languedoc (Canal du Midi). -
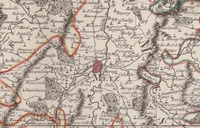 Carte de la Lorraine, du Barrois et des Trois Evêchés de Metz, Toul et Verdun. Divisée par Baillages, Dans laquelle se trouve Comprise la Généralité de Metz. Dressée par DezaucheCarte politique; 1790;
Limites des départements de la Moselle, de la Meuse, de la Meurthe et des Vosges. Dressée par Dezauche [Jean-Claude Dezauche (1745-1829)], ingénieur Géographe. Successeur des Srs Delisle [Guillaume Delisle (1675-1726)] et Phil. Buache [Philippe Buache (1700-1773)], premiers géographes de l'Académie des sciences. Échelles, 7 Grandes Lieues de France de 20 au Degré [=Om. 112 ; 1:342 000 environ]
Carte de la Lorraine, du Barrois et des Trois Evêchés de Metz, Toul et Verdun. Divisée par Baillages, Dans laquelle se trouve Comprise la Généralité de Metz. Dressée par DezaucheCarte politique; 1790;
Limites des départements de la Moselle, de la Meuse, de la Meurthe et des Vosges. Dressée par Dezauche [Jean-Claude Dezauche (1745-1829)], ingénieur Géographe. Successeur des Srs Delisle [Guillaume Delisle (1675-1726)] et Phil. Buache [Philippe Buache (1700-1773)], premiers géographes de l'Académie des sciences. Échelles, 7 Grandes Lieues de France de 20 au Degré [=Om. 112 ; 1:342 000 environ] -
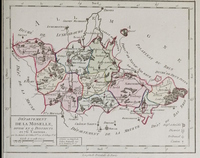 Atlas national portatif de la France, destiné a l'instruction publique, composé de 93 cartes et d'un précis méthodique et élémentaire de la nouvelle géographie du royaume, dédié et présenté à l'Assemblée nationaleCarte politique; 1792; Dumez, Pierre (1757-1794); Chanlaire, Pierre Gilles (1758-1817);
L'atlas au format 22x29 cm in-quarto est composé de 93 cartes, dont 3 repliées, représentation des départements nouvellement créés. Il parait sous la direction de Pierre Dumez (1757-1794), directeur du Bureau de l'Atlas, secondé de Pierre-Grégoire Chanlaire, géographe, géomètre. Parmi les cartes disponibles, figure celle de la Moselle, divisée en 9 district et 76 cantons. L'atlas est plusieurs fois édité, de 1789 à 1796.
Atlas national portatif de la France, destiné a l'instruction publique, composé de 93 cartes et d'un précis méthodique et élémentaire de la nouvelle géographie du royaume, dédié et présenté à l'Assemblée nationaleCarte politique; 1792; Dumez, Pierre (1757-1794); Chanlaire, Pierre Gilles (1758-1817);
L'atlas au format 22x29 cm in-quarto est composé de 93 cartes, dont 3 repliées, représentation des départements nouvellement créés. Il parait sous la direction de Pierre Dumez (1757-1794), directeur du Bureau de l'Atlas, secondé de Pierre-Grégoire Chanlaire, géographe, géomètre. Parmi les cartes disponibles, figure celle de la Moselle, divisée en 9 district et 76 cantons. L'atlas est plusieurs fois édité, de 1789 à 1796. -
 Décret sur l'établissement des écoles normales, du 9 brumaire an III (30 octobre 1794)Article législatif; Lois et règlements; 1794; Lakanal, Joseph (1762-1845); Convention nationale;
L'École normale, dite « de l'an III » désigne un ensemble de cours destinés à former des enseignants à Paris, pendant une durée de quatre mois. Instituée en l'an III par la Convention, l'école est créée sur l’impulsion de Dominique Joseph Garat, de Joseph Lakanal et du Comité d'instruction publique de la Convention. Les instituteurs devaient une fois formés répandre l'instruction en province en ouvrant à leur tour des écoles normales dans les départements et districts. Seule la première des sessions prévues eut lieu durant la période prévue, du 1er pluviose de l'an III (20 janvier 1795) au 30 floréal de l'an III (19 mai 1795). L'École normale de l'an III est généralement considérée comme l’ancêtre de l’École normale supérieure (rue d'Ulm à Paris) et des autres écoles normales françaises. L’école, prévue pour près de 1 500 élèves, s’installe dans un amphithéâtre du Muséum national d'histoire naturelle, trop petit pour accueillir toute la promotion. Elle réunit des professeurs brillants, parmi ceux-ci en mathématiques : Joseph-Louis Lagrange et Pierre-Simon Laplace, en géométrie descriptive : Gaspard Monge. Napoléon crée ensuite par décret du 17 mars 1808 un «pensionnat normal» au sein de l'Université de France pour «former à l'art d'enseigner les lettres et les sciences». L'école est rouverte de 1810 à 1822.
Décret sur l'établissement des écoles normales, du 9 brumaire an III (30 octobre 1794)Article législatif; Lois et règlements; 1794; Lakanal, Joseph (1762-1845); Convention nationale;
L'École normale, dite « de l'an III » désigne un ensemble de cours destinés à former des enseignants à Paris, pendant une durée de quatre mois. Instituée en l'an III par la Convention, l'école est créée sur l’impulsion de Dominique Joseph Garat, de Joseph Lakanal et du Comité d'instruction publique de la Convention. Les instituteurs devaient une fois formés répandre l'instruction en province en ouvrant à leur tour des écoles normales dans les départements et districts. Seule la première des sessions prévues eut lieu durant la période prévue, du 1er pluviose de l'an III (20 janvier 1795) au 30 floréal de l'an III (19 mai 1795). L'École normale de l'an III est généralement considérée comme l’ancêtre de l’École normale supérieure (rue d'Ulm à Paris) et des autres écoles normales françaises. L’école, prévue pour près de 1 500 élèves, s’installe dans un amphithéâtre du Muséum national d'histoire naturelle, trop petit pour accueillir toute la promotion. Elle réunit des professeurs brillants, parmi ceux-ci en mathématiques : Joseph-Louis Lagrange et Pierre-Simon Laplace, en géométrie descriptive : Gaspard Monge. Napoléon crée ensuite par décret du 17 mars 1808 un «pensionnat normal» au sein de l'Université de France pour «former à l'art d'enseigner les lettres et les sciences». L'école est rouverte de 1810 à 1822. -
 Programmes de l'enseignement polytechnique de l'École centrale des travaux publics [7 pluviôse an III, 15 février 1795]Fascicule; Lois et règlements; Programme d'enseignement; 1795-02; Convention nationale;
Daté du 7 pluviôse an III, 15 février 1795, le premier programme de l'école est établi en vertu des décrets de la Convention nationale du 21 ventôse an II (11 mars 1794), et du 7 vendémiaire an III (28 septembre 1794). Un exemplaire détenu par la bibliothèque Newberry de Chicago a été numérisé et peut être consulté sur Internet Archive.
Programmes de l'enseignement polytechnique de l'École centrale des travaux publics [7 pluviôse an III, 15 février 1795]Fascicule; Lois et règlements; Programme d'enseignement; 1795-02; Convention nationale;
Daté du 7 pluviôse an III, 15 février 1795, le premier programme de l'école est établi en vertu des décrets de la Convention nationale du 21 ventôse an II (11 mars 1794), et du 7 vendémiaire an III (28 septembre 1794). Un exemplaire détenu par la bibliothèque Newberry de Chicago a été numérisé et peut être consulté sur Internet Archive. -
 Décret portant établissement d'écoles centrales pour l'enseignement des sciences, des lettres et des arts, du 7 ventôse an III (25 février 1795)Article législatif; Lois et règlements; Texte transcrit; 1795-02; Convention nationale; Lakanal, Joseph (1762-1845);
L'organisation d'"écoles secondes" devient régulièrement discuté à la Convention dès mars 1794. Le terme finalement retenu sera celui d'École centrale. Le projet de loi est présenté par Lakanal à la Convention le 26 frimaire an III (16 décembre 1794). Il devient adopté le 7 ventôse an III (25 février 1795), avec deux modifications intégrées dans le texte ici transcrit. Parmi les professeurs prévus figurent un professeur de mathématiques, un professeur de physique et de chimie expérimentales; un professeur d’arts et métiers; un professeur des arts de dessin. Le Titre II de la loi Daunou portant sur l'organisation de l'enseignement en général viendra apporter en 12 articles des précisions sur les enseignements dispensés, le mode de sélection des professeurs par un jury d’instruction, les conditions d'admission des élèves, la répartition des écoles centrales sur le territoire.
Décret portant établissement d'écoles centrales pour l'enseignement des sciences, des lettres et des arts, du 7 ventôse an III (25 février 1795)Article législatif; Lois et règlements; Texte transcrit; 1795-02; Convention nationale; Lakanal, Joseph (1762-1845);
L'organisation d'"écoles secondes" devient régulièrement discuté à la Convention dès mars 1794. Le terme finalement retenu sera celui d'École centrale. Le projet de loi est présenté par Lakanal à la Convention le 26 frimaire an III (16 décembre 1794). Il devient adopté le 7 ventôse an III (25 février 1795), avec deux modifications intégrées dans le texte ici transcrit. Parmi les professeurs prévus figurent un professeur de mathématiques, un professeur de physique et de chimie expérimentales; un professeur d’arts et métiers; un professeur des arts de dessin. Le Titre II de la loi Daunou portant sur l'organisation de l'enseignement en général viendra apporter en 12 articles des précisions sur les enseignements dispensés, le mode de sélection des professeurs par un jury d’instruction, les conditions d'admission des élèves, la répartition des écoles centrales sur le territoire. -
 Constitution du 5 fructidor an III (22 aout 1795)Article législatif; Lois et règlements; Texte transcrit; 1795-08; Convention nationale;
Votée par la Convention plus d'un an après la chute de Robespierre, la Constitution de la République française du 5 fructidor an III (22 août 1795) est fondatrice de la Première République française. La période du Directoire qui en résulte met fin à la période révolutionnaire. Adoptée par la Convention thermidorienne, approuvée par référendum le 20 fructidor de l'an III (6 septembre), elle est promulguée par une loi du 6e jour complémentaire an III (22 septembre), qui la proclame loi fondamentale de l’État. Elle a pour préambule la Déclaration des droits et des devoirs de l'homme et du citoyen, en son texte de 1795. La constitution de l'an III entre en vigueur en brumaire an IV (octobre 1795), avec la mise en place des nouveaux pouvoirs. Dans cette constitution, les députés de la Convention séparent les pouvoirs législatif et exécutif. Le pouvoir législatif est confié à un corps constitué du Conseil des Cinq-Cents et du Conseil des Anciens, au nombre de 250, ainsi nommés parce qu'ils doivent avoir plus de 40 ans. Les Cinq-Cents émettent des propositions de lois. Les Anciens votent sur ces propositions pour les transformer en lois. Dans le système bicaméral adopté, les deux assemblées sont renouvelées par tiers tous les ans. Le pouvoir exécutif est confié à un Directoire de cinq membres âgés d'au moins 40 ans. Chaque année, l'un d'eux est changé par tirage au sort. Les Directeurs sont désignés par les Anciens sur une liste de dix candidats proposés par les Cinq-Cents. Tous anciens conventionnels, les premiers Directeurs furent Paul Barras, Jean-François Reubell, Louis-Marie de La Révellière-Lépeaux, Lazare Carnot et Étienne-François Le Tourneur. Assistés de ministres qui assurent le fonctionnement de l'administration, les Directeurs se réservent les tâches proprement gouvernementales. Cette constitution donne des obligations à l'État en matière d'enseignement primaire. L'article 16 du titre II "État politique des citoyens de la constitution" précise : « Les jeunes gens ne peuvent être inscrits sur le registre civique, s'ils ne prouvent qu'ils savent lire et écrire, et exercer une profession mécanique. Les opérations manuelles de l'agriculture appartiennent aux professions mécaniques. — Cet article n'aura d'exécution qu'à compter de l'an XII de la République ». L'an XII correspond aux années 1803 et 1804 du calendrier classique. La question de l'instruction publique est traitée plus amplement dans le titre X, articles 296 à 301. Il y est précisé la division entre instruction primaire locale, instruction secondaire départementale, institut national. Le terme d'Académie nationale est soigneusement évité car rappelant trop l'Académie royale. Cette dernière avait été supprimée en aout 1793. Autorisation est donnée à l'ouverture d'écoles privées. Les constitutions suivantes ne comprendront ni précisions sur les divisions territoriales, ni réglementations sur l'instruction publique et privée, cela faisant l'objet de lois longuement débattues en assemblées.
Constitution du 5 fructidor an III (22 aout 1795)Article législatif; Lois et règlements; Texte transcrit; 1795-08; Convention nationale;
Votée par la Convention plus d'un an après la chute de Robespierre, la Constitution de la République française du 5 fructidor an III (22 août 1795) est fondatrice de la Première République française. La période du Directoire qui en résulte met fin à la période révolutionnaire. Adoptée par la Convention thermidorienne, approuvée par référendum le 20 fructidor de l'an III (6 septembre), elle est promulguée par une loi du 6e jour complémentaire an III (22 septembre), qui la proclame loi fondamentale de l’État. Elle a pour préambule la Déclaration des droits et des devoirs de l'homme et du citoyen, en son texte de 1795. La constitution de l'an III entre en vigueur en brumaire an IV (octobre 1795), avec la mise en place des nouveaux pouvoirs. Dans cette constitution, les députés de la Convention séparent les pouvoirs législatif et exécutif. Le pouvoir législatif est confié à un corps constitué du Conseil des Cinq-Cents et du Conseil des Anciens, au nombre de 250, ainsi nommés parce qu'ils doivent avoir plus de 40 ans. Les Cinq-Cents émettent des propositions de lois. Les Anciens votent sur ces propositions pour les transformer en lois. Dans le système bicaméral adopté, les deux assemblées sont renouvelées par tiers tous les ans. Le pouvoir exécutif est confié à un Directoire de cinq membres âgés d'au moins 40 ans. Chaque année, l'un d'eux est changé par tirage au sort. Les Directeurs sont désignés par les Anciens sur une liste de dix candidats proposés par les Cinq-Cents. Tous anciens conventionnels, les premiers Directeurs furent Paul Barras, Jean-François Reubell, Louis-Marie de La Révellière-Lépeaux, Lazare Carnot et Étienne-François Le Tourneur. Assistés de ministres qui assurent le fonctionnement de l'administration, les Directeurs se réservent les tâches proprement gouvernementales. Cette constitution donne des obligations à l'État en matière d'enseignement primaire. L'article 16 du titre II "État politique des citoyens de la constitution" précise : « Les jeunes gens ne peuvent être inscrits sur le registre civique, s'ils ne prouvent qu'ils savent lire et écrire, et exercer une profession mécanique. Les opérations manuelles de l'agriculture appartiennent aux professions mécaniques. — Cet article n'aura d'exécution qu'à compter de l'an XII de la République ». L'an XII correspond aux années 1803 et 1804 du calendrier classique. La question de l'instruction publique est traitée plus amplement dans le titre X, articles 296 à 301. Il y est précisé la division entre instruction primaire locale, instruction secondaire départementale, institut national. Le terme d'Académie nationale est soigneusement évité car rappelant trop l'Académie royale. Cette dernière avait été supprimée en aout 1793. Autorisation est donnée à l'ouverture d'écoles privées. Les constitutions suivantes ne comprendront ni précisions sur les divisions territoriales, ni réglementations sur l'instruction publique et privée, cela faisant l'objet de lois longuement débattues en assemblées.