-
Type
-
Livre
-
Cours de mécanique
-
Description
-
1767. Paris. JBG Musier, 467 pages, 11 planches, 203 figures, pas de table des matières
1770. Paris. JBG Musier, 479 pages, 11 planches, 203 figures, pas de table de données, table des matières, leçons 376 à 735
1772. Paris. JBG Musier, non numérisé,
1788. Paris. PH.-D. PIERRES, 480 pages, 13 planches, 128 figures, 8 tables de données, leçons 350 à 854,
-
Date
-
1767
-
1770
-
1772
-
1777
-
1788
-
Editeur
-
Paris : J.B.G. MUSIER fils, Libraire, quai des Augustins, à Saint Etienne. 1767, 1770, 1777
-
Paris : DE L'IMPRIMERIE DE PH.-D. PIERRES, Premier Imprimeur Ordinaire du Roi, rue S. Jacques. 1788
-
Table des matières
-
D'après l'édition de 1788 PH.-D. PIERRES
480 pages, 13 planches, 8 tables, leçons de 350 à 854
Biblioteca Provinciale di Napoli, Google
[p470]
TABLE DES MATIERES
APPLICATIONS des principes généraux de la Mécanique à différens cas de mouvement & d'équilibre, 1
Du choc direct des corps, 1
Du choc direct des corps durs, 2
Règle générale pour trouver la vitesse après le choc, 6
Réflexions sur la force d'inertie, 6
Cette force diffère des forces actives, en ce que le mouvement perdu par l’un des corps, n’est point entièrement perdu, mais il passe à l’autre corps, 7
Elle ne dépend ni de la pesanteur, ni de la résistance de l'air; c'est une force particulière à la matière, & qui, se fait sentir proportionnellement à la masse ou au nombre des parties matérielles, 9
Quelques applications du choc des corps durs; conséquences qui en résultent par rapport à la percussion, 10
La force d’un corps en mouvement, ne peut être mesurée par des poids, 14
Remarques sur les forces vives, 18
Que la différence de sentimens qui a partagé les Mathématiciens pendant quelque temps, sur la meure des forces des corps en mouvement, ne tient qu’à la différente acception du mot force, chez les uns & les autres, & n'intéresse en rien la Mécanique, 21
Du choc direct des corps élastiques, 23
[p471]
Règle générale pour avoir la vitesse après le choc des corps élastiques, 25
La vitesse relative des corps élastiques, est la même, après le choc, qu’auparavant, 30
Du choc & de la résistance des fluides, 30
La résistance faite aux surfaces planes, mues directement, est en raison composée de la densité du milieu, de l’étendue de la surface, & du quarré de la vitesse, 33
Mesure du choc ou de la résistance absolue des fluides; différens sentimens sur ce point, 37
Modifications à la loi générale de résistance précédemment établie, 39
Choc des fluides peut être comparé au poids des corps, 39
Le choc instantané de deux corps, dans un fluide, se fait comme dans un milieu libre, 40
De la résistance sur les surfaces planes obliques, 43
De la résistance qu’éprouve un solide de révolution, mu suivant son axe, 54
Application à la sphère, 56
Du mouvement rectiligne des corps dans les milieux résistans, 57
Application à l’une des expériences faites à Londres par Newton, 64
De la vitesse que les projectiles peuvent recevoir par l’action d’un fluide élastique condensé, tel que l’air ou la poudre enflammée, 71
Du rapport de la charge , à la longueur de la pièce, pour que la vitesse soit la plus grande possible, 78
Autres considérations nécessaires pour résoudre pleinement la question de la vitesse des projectiles au sortir de la pièce, 79
De la force du recul dans les armes à vent où à feu, 88
Du mouvement des corps pesans le long des plans inclinés, 88
Rapport de la vitesse, le long du plan incliné, à la vitesse contemporaine, suivant la verticale, 92
[p472]
Espaces décrits en même temp par la chute verticale & par la çhute le long des plans différemment inclinés, 93
Égalité entre le temps de la chute par le diamètre vertical d’un cercle & le temps de la chute par une sourandante quelconque, tirée d’une extrémité de ce diamètre, 94
Rapport des temps des chutes Je long de plans différemment inclinés & de même hauteur, 95
Rapport des vitesses acquises par des çhutes le long de plans différemment inclinés & de même hauteur, 96
Du mouvement le long des surfaces courbes, 96
La vitesse acquise en tombant le long d'un arc de courbe quelconque, est la même que çelle qui auroit été acquise en tombant verticalement de la même hauteur, 100
Rapport des vitesses acquises par des chutes le long d'arcs
de cercle, 103
Du mouvement d’oscillation, 104
Les oscillations qui se font dans des arcs d'un petit nombre de degrés, sont sensiblement de même durée entre elles, 107
Pendule simple ; ce qu’on entend par là, 107
Rapport des durées des oscillations , avec les longueurs des pendules & l’intensité de la pesanteur, 109
Rapport du nombre des vibrations, 110
Longueur du pendule qui bat les secondes à Paris, 111
Comment elle sert à déterminer la quantité dont un corps pesant doit tomber dans la première seconde de sa chute, sans la résistance de l'air, 112
Le temps de la chute par l’arc de cercle, plus court que le temps de la chute par la corde du même arc, 113
Du mouvement en ligne courbe, en général, 113
Du mouvement dans le cercle & de la force centrifuge, 117
Rapport de la force centrifuge d'un çorps qui circule, à son poids, 119
Comparaisons des forces centrifuges entr’elles, 124
[p473]
Du mouvement des projectiles dans le vide, 128
La courbe décrite dans le vide , par les projectiles, est une parabole, 132
Comment on la détermine à aide de l’angle, & de la vitesse de projection, 133
Comment on détermine l’amplitude du jet, où la portée, 136
La plus grande portée dans le vide, est sous 45 degrés; & à distances égales de part & d'autre de 45 degrés, les portées sont égales, 137
Rapports des portées, 138
Quelle seroit la portée de but en blanc dans le vide, 140
Comment on détermine l’inclinaison qu’on doit donner au mortier pour faire tomber une bombe sur un objet proposé, 143
Il y a toujours deux inclinaisons propres à cet effet, 144
Des ricochets, 147
Du mouvement des projectiles dans les milieux résistans, 153
Quoique l’air soit un fluide fort rare, la résistance au mouvement des projectiles en usage dans l’Artillerie, n’en altère pas moins considérablement les portées, 154
Table d'épreuves de portées d'une pièce de 24, chargée à 9 livres de poudre , de laquelle il résulte qu'en regardant comme nulle la résistance faite à la portée sous 15 degrés, la portée observée sous 45 degrés n'est que les 2/3 de ce qu’elle auroit dû être si l'air n'eut pas résisté, & qu’elle est de près de 1000 toises plus courte que celle-ci, 155
Et comme la portée observée sous 15 degrés a elle-même été altérée par la résistance de l'air, il s'ensuit que la portée sous 45 degrés, l’a été beaucoup plus qu’il ne résulte de cette première comparaison, 156
Comment on détermine les équations qui servent à trouver les circonstances du mouvement des projectiles dans les milieux résistans, 157
[p474]
Les méthodes ordinaires d’approximation sont insuffisantes pour déterminer la courbe, lorsque la vitesse de projection est grande, 164.
Manière de lever cette difficulté, 166
Équation très-approchée de la courbe décrite par les projectiles dans un milieu résistant, 174
Comparaison de cette théorie avec l'expérience, 176
Comment on en conclud la force de la poudre dans les épreuves rapportées à la p 155, 177
La portée observée sous 15 degrés, suppose que le boulet parti avec une vitesse à parcourir 1393 pieds ou 233 toises par seconde, dans le vide, 180
Manière de calculer les portée relatives aux autres épreuves contenues dans la Table de la page 155, 181
Table de comparaison des portées calculées, avec les portées observées, 185
Table des plus grandes hauteurs auxquelles le boulet a dû s'élever dans ces épreuves, 191
De la manière de calculer la durée des portées, 191
Application à quelques épreuves faites à Strasbourg en 1766, 193
La résistance de l'air, dans ces épreuves, au sortir de la pièce, étoit d'environ huit fois le poids du boulet, 195
Table des durées des portées dans l’air & dans le vide, en vertu de la force de la poudre que supposent les épreuves rapportées à la page 155, 196
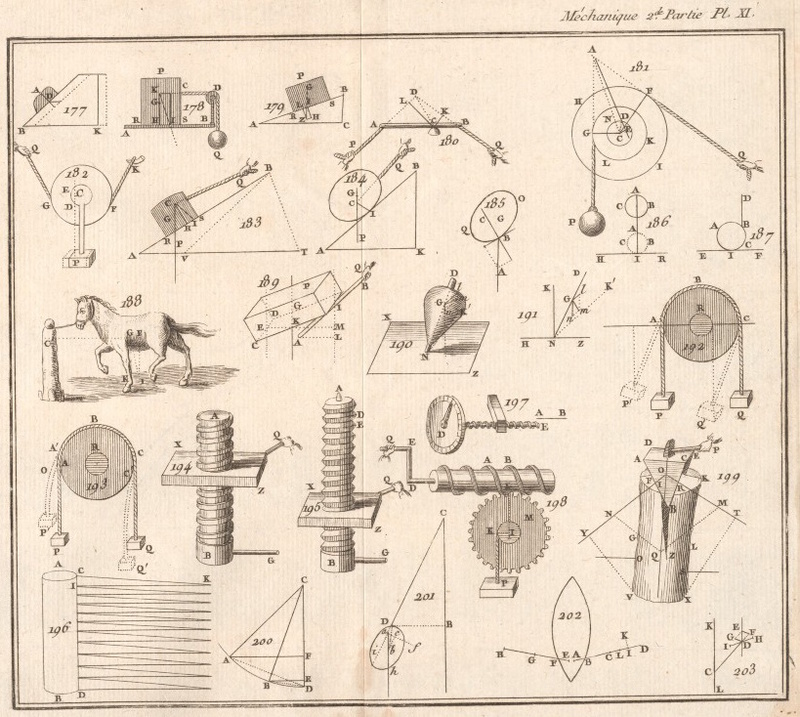
DE L'ÉQUILIBRE ET DU MOUVEMENT DANS LES MACHINES
Le nombre des machines simples, peut être réduit à cinq, savoir, les cordes, le levier, la poulie, le treuil & de plan incliné, 200
Des cordes, 201
Équilibre entre trois forces appliquées à trois cordons assemblés par un même nœud, 201
[p475]
Rapports de ces forces, 203
Condition de l'équilibre lorsqu'une des forces agit à l’aide d'un anneau qui peut glisser sur la corde à laquelle les deux autres forces sont appliquées, & lorsqu'une corde tisée par deux puissances est retenue par un point fixe qu'elle embrasse, 207
Équilibre entre tant de puissances qu'on voudra, qui agissent les unes contre les autres à l'aide de cordes seulement, & rapports des forces, 209
Comment, & dans quels cas, on peut varier les rapports ou les directions des puissances, sans troubler l’équilibre, 213
Comment le poids des cordes change la communication de l’action des puissances, 218
Des poulies & des moufles, 222
Comment se fait l'équilibre sur la poulie, 223
Rapports des tensions des cordons qui embrassent la poulie, à l'effort que supporte le centre, 224
Autre manière d'envisager l’équilibre sur la poulie, 226
Des moufles, 229
Rapport de la puissance au poids sur les moufles, 229
Du levier, lorsque les forces qui lui sont appliquées sont toutes dans an même plan, 234
Équilibre entre deux puissances appliquées à un levier, 235
Rapport de ces deux puissances, 237
Autres rapports, 238
Leviers de différentes espèces, 240
Remarques sur le point d'appui, 241
Différence entre l'équilibre des poids, & l'équilibre des corps animés de vitesses finies, 245
Équilibre entre deux puissances appliquées à un levier, 247
Propriété générale de cet équilibre, 249
Comment on a égard au poids du levier, & différentes applications, 250
De la balance & des conditions de sa construction, 253
[p476]
Du levier en mouvement, des centres de percussion , des centres d'oscillation, & du choc excentrique des corps, 260
Comment on détermine la vitesse de rotation que doit prendre un corps fixé par un de ses points , & sollicité par plusieurs forces qui agissent dans un mème plan, 263
Comment on trouve la résultante & le point où passe la résultante des mouvemens de rotation d’un corps assujetti à tourner autour d’un axe fixe, 266
Ce que c’est que le moment d'inertie des corps, 267
Ce que c'est que le centre de percussion, & comment on le détermine, 270
Ce que c'est que le centre d'oscillation, & comment on le détermine, 270
Exemple du choc excentrique, 272
Comment on détermine le moment d'inertie des corps, 274
Du point où il faudroit placer un corps, pour qu'il reçût d'une verge, tournant autour d'un point fixe, la plus grande force possible, 281
Du centre de percussion & d'oscillation d’une sphère, 282
Autre exemple du choc excentrique, 286
Centre spontané de rotation; ce que c'est, & comment on le détermine, 290
Du tour ou treuil, cabestan, &c 291
Comment se fait l'équilibre dans cette machine, 294
Rapport de la puissance au poids, 295
Quelques applications, p. 298.
Rapport du rayon de la roue à celui du cylindre, pour que, dans le cas du mouvement, la force communiquée soit la
plus grande possible, 299
Quelques autres applications du tour, 301
Des roues dentées, 305
Comment elles servent à augmenter la force dans un rapport donné, 305
Comment elles servent à augmenter la vitesse dans un rapport donné, 306
[p477]
Applications, 308
De l'équilibre sur les plans, 311
Conditions de cet équilibre sur un plan, 311
Rapport de la puissance au poids, dans le cas de l’équilibre sur un plan incliné, 314
Autres manières d'exprimer ce rapport, 314
Rapport que doivent avoir deux puissances pour être égale- ment propres à soutenir un même poids sur un même plan incliné, 316
Quelle est la plus petite puissance qu'on puisse employer pour soutenir un corps sur un plan incliné, 318
Quand un corps ne repose sur un plan que par un où deux points seulement, on peut déterminer la pression que supporte chaque point; mais s’il repose par plus de deux points la pression de chacun est indéterminée, 321
Rapport de deux poids qui se font équilibre sur deux plans inclinés, à l’aide d’une corde qui les joint, 322
Rapport de deux poids qui se font équilibre sur deux plans inclinés, à l’aide d’une corde passant sur une poulie de renvoi, 322
Conditions de l'équilibre d’un poids qui repose sur plusieurs plans à la fois, 323
Application aux voûtes, 324
Du mouvement sur les plans, 325
De la vis, 327
Pas de la vis, ce que c'est, 328
Génération de la vis, 328
Équilibre sur cette machine, 329
Rapport de la puissance au poids, 331
Quelques applications, 333
Du coin, 334
Considéré comme un instrument à fendre, sa théorie est encore fort imparfaite, 334
Conditions de l'équilibre dans cette machine, 335
Rapport de la puissance aux résistances des partes à séparer, 337
Du frottement, 339
Ce que l'expérience apprend sur le frottement, 341.
Comment on peut déterminer Ia valeur du frottement, pa l'expérience, 346
[p478]
Condition, pour qu'un corps reste en équilibre sur une surface proposée, eu égard au frottement, 349
Angle du frottement; ce que c'est, 350
Frottement sur le levier, dont l'appui est considéré comme un simple soutien, 351
Frottement sur le levier, dont l'appui est un boulon; & en général, du frottement sur le tour, 352
Charge des appuis de cette Machine, 356
Frottement dans le tour , ayant égard au poids de la machine, au diamètre & au poids des cordes, 361
Application à la poulie fixe, 364
Frottement dans la poulie mobile, 366
Frottement dans les moufles, 371
Règle peur déterminer l'éffet de ce frottement, lorsque le poids de la machine est petit, par rapport à celui que la machine doit élever, 373
Application de cette règle, 374
Frottement dans les moufles; eu égard au poids de toutes les parties de la machine 376.
Application à la chèvre, pour calculer la force nécessaire pour élever avec cette machine, une pièce de 4, 378
Manière plus générale de déterminer le rapport de deux puissances qui se font équilibre sur le tour, eu égard au frottement & au poids de toutes les parties de la machine, 384
Frottement sur le plan incliné, 394
Frottement des roues de voitures contre le terrein, & de l’essieu contre les boîtes, 397
De quelle manière l'action du cheval & le poids de la voiture se distribuent, & ce qu’il faut pour déterminer le rapport de ces deux forces dans le cas du frottement, 399
Comment on peut déterminer la plus petite force possible qui puisse vaincre ce frottement, 405
[p479]
Différence dans la manière dont on doit envisager cette question , dans le cas où il s'agit de faire rouler la voiture, & dans le cas où il s'agit de faire passer la roue sur un obstacle, 410
Autres applications du frottement, 411
Frottement d’une corde roulée sur une surface courbe, 416
Application, 419
Comment on peut déterminer, par expérience , l'angle du frottement , relatif à cette espèce de frottement, 420
De la roideur des cordes, 421
De la manière d'estimer les forces appliquées aux machines, 426
APPENDICE où l’on traite plus particulièrement du mouvement des Projectiles dans un milieu résistant.
QUE la première méthode de calculer les portées, les donne trop fortes, 439
Que néanmoins elle écarte peu du vrai, 440
Que sans avoir. recours à la seconde méthode que l'on donne ensuite, on peut approcher davantage de la véritable valeur des portées, en calculant séparément la branche ascendante & la branche descendante, 443
De la manière d'avoir égard au changement de densité dans le calcul des portées, par la première méthode, 443
Table des nombres nécessaires dans le calcul du mouvement des projectiles dans les milieux résistans, 454
Table de comparaison entre la théorie & l'expérience , pour des bombes de 11po. (pouces), 10 lig. (lignes) de diamètre, du poids de 141£, & chassées avec 3£1/4 de poudre, 456
Que les épreuves rapportées dans cette Table, font connoître que la bombe étoit chassée avec une vitesse à parcourir 366 pieds par seconde, dans le vide, 456
Table de comparaison entre la théorie & l'expérience pour
[p480]
Table de comparaison entre la théorie & l'expérience pour des boulets de 14, chassés avec 8£1/2 de poudre, 460
Que la vitesse de ces boulets au sortir de la pièce, étoit une vitesse à parcourir 1262 pieds par seconde, dans le vide, 458
Que la résistance de l'air altère tellement les portées, que son effet, selon l'expérience, a diminué la portée sous 45d (degrés), de 6732 toises sur 8786; & selon la théorie, de 6802 sur 8786, 459
Comment on détermine plus rigoureusement l'équation de la courbe décrite par les projectiles dans les milieux résistans, 461
Comment on emploie cette méthode pour avoir égard au changement de densité, 467
Fin de la Table des Matières
EXTRAIT DES REGISTRES. DE L'ACADÉMIE ROYALE DES SCIENCES. Du 11 Décembre 1771.
-
Titre
-
V. Cours de mathématiques à l'usage des Gardes du Pavillon et de la Marine. Suite de la quatrième partie. Contenant l'Application des principes généraux de la Méchanique à différents cas de mouvement & d'équilibre
Bézout, Étienne (1730-1783)
VI. Suite du cours de mathématiques à l'usage des Gardes du pavillon et de la Marine. Contenant le Traité de navigation.
IV. Cours de mathématiques à l'usage des Gardes du Pavillon et de la Marine. Quatrième partie. Contenant les Principes généraux de la Mécanique, précédés des Principes de calcul qui servent d'introduction aux Sciences physico-mathématiques